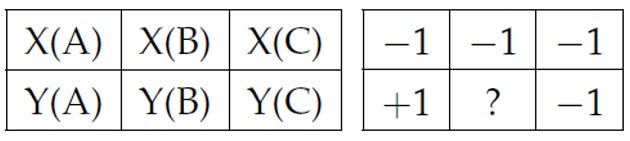Contextuality
And the silliest famous proof (or the most famous silly proof)
One of the most significant features of the quantum theory is its contextuality, and the first to recognize and stress this was Niels Bohr.
The theory does, in fact, feature two kinds of contextuality. The first denotes the fact that the measurable properties of quantum objects (like atoms and subatomic particles) are defined by the ways in which they are measured, and that they only exist if and when they are measured. The second, unknown in Bohr’s time, only becomes a thing if one insists that the measurable properties of quantum objects also exist when they are not measured. On that hypothesis, the value of a measurable quantity will generally be contextual in the sense that it depends on which other quantity or quantities it is measured together with. As an example recall Quantum quandary #2, and assume that the values of five of the six quantities involved are as given in the table on the right:
What will the value of Y(B) be? If it is measured together with X(A) and Y(C), then it has to be +1 since the product X(A) Y(B) Y(C) will come out equal to +1 whenever these three quantities are measured. If Y(B) is measured together with Y(A) and X(C) instead, then it has to be -1 since the product Y(A) Y(B) X(C) also has to come out equal to +1 whenever the three quantities are measured. There’s a delicious irony here: one insists that the properties of quantum objects have values whether or not they are measured, and one finds that their values generally depend on which other properties are measured at the same time. Bohr would have been tickled pink by the inescapability of contextuality, had he lived to see it proven (in, by now, many different ways).
For context (no pun intended): In 1932, the mathematician John von Neumann published an immensely influential book, in which he presented what appeared to be a formal proof that the statistical predictions of quantum mechanics cannot be reproduced by any theory that features unmeasured properties (also known as “hidden variables”). Fast forward to the late 1940s. Having just obtained two bachelor's degrees at the University of Belfast, John Steward Bell wondered whether such variables could be added to quantum mechanics despite what the “three musketeers of the Copenhagen Interpretation” (by which he meant Niels Bohr, Werner Heisenberg, and Wolfgang Pauli) had decreed. Reading a popular account of the quantum theory by one of its chief architects (Max Born), he learned two things: (i) that back in the late 1920s one of the theory’s founders (Louis de Broglie) had already tried to invent a hidden-variables scheme, and (ii) that von Neumann had subsequently published a proof demonstrating that hidden variables could not be made compatible with quantum mechanics. Impressed by von Neumann’s alleged proof and unable to read the German original, Bell dropped the idea.
Then, in 1952, he “saw the impossible done.” The year before, David Bohm had presented a version of von Neumann’s proof in his influential textbook, and had agreed with von Neumann that hidden-variable interpretations of quantum theory were impossible. The very next year, Bohm published two papers in which he suggested an interpretation of quantum mechanics in terms of hidden variables! Bell nevertheless found it prudent, for the sake of his academic career, to walk away from foundational questions — until he arrived at CERN, the famous particle-physics laboratory near Geneva. There he made the acquaintance of Josef Jauch, who at the time was trying to strengthen von Neumann’s proof. To Bell, this was like waving a red flag in front of a bull. He resolved to discover where von Neumann had erred. What he found was that von Neumann had made an assumption that could only be described as silly. In an interview given in 1988, this is what he said:
The von Neumann proof, if you actually come to grips with it, falls apart in your hands! There is nothing to it. It’s not just flawed, it’s silly!... You may quote me on that: The proof of von Neumann is not merely false but foolish!
By the time Bell’s exposure of von Neumann’s blunder appeared in print, a third of a century had passed. All this while von Neumann’s argument appears to have been examined neither by physics students nor, as David Mermin put it, by “those who appealed to it to rescue them [the students] from speculative adventures.”
So what was the silly mistake? It was to assume that the measurement of a physical quantity must yield a value that is independent of what other quantities are measured simultaneously. If two observables A and B are compatible with a third observable C but fail to be compatible with each other — which means that A and C can be measured together, and B and C can be measured together, but A cannot be measured together with B — then it is excessive to require that the value of C revealed by a simultaneous measurement of A and C must be the same as that revealed by a simultaneous measurement of B and C. What von Neumann had actually proved was not that there can be no hidden-variables version of quantum mechanics but only that there can be no non-contextual hidden-variables version.
The contextuality of quantum mechanics has a momentous consequence: it makes it impossible to conceive either of macroscopic objects or of the microscopic objects of which the former are commonly said to be composed as substances in the philosophical sense of the term. Atoms and subatomic particles cannot be substances because they depend on experimental arrangements for their properties, and if microscopic objects cannot be substances then neither can the objects that we tend to think of as composed of them.
The philosophical concept of substance, as was mentioned in a previous mailing, mostly stands for either of two ideas. While the Lockean kind of substance serves as a conceptual glue which binds together different properties in much the same way a single logical or grammatical subject joins different predicates, the Aristotelean kind serves to bestow independent existence on Lockean substances (i.e., on bundles of properties). To Aristotle, whatever could be the predicate of a logical or grammatical subject was a property, and whatever could not be predicated of anything else was a substance. Properties therefore owed their existence to being attributes of substances, while substances owed their existence to nothing but themselves. The implication of contextuality is that neither macroscopic objects nor their so-called microscopic “constituents” can be thought of as existing independently of those by whom they are perceived and/or conceived — and this means us.
In point of fact, the very macro/micro distinction hinges on how the two kinds of objects relate to human experience. Objects are macroscopic to the extent that they are accessible to direct sensory experience; they are microscopic to the extent that they are not. To the extent that objects are accessible to direct sensory experience, we can speak of them in the familiar language of things that interact with each other and change in accordance with causal laws. To the extent that they are not, we can only speak of them indirectly, by speaking of events that can be described in the familiar object-oriented language, or by speaking of correlations between such events. The reason we can speak of microscopic objects only indirectly is that all physical concepts that are not purely mathematical owe their meanings at least in part to the spatiotemporal structure of human sensory experience. There is no guarantee that these concepts make sense when applied to a reality beyond the reach of human sensory experience.
On the usual postulation of a spatiotemporal physical expanse (“spacetime”) that both depends and does not depend on the human mind, I will say more in a future mailing. (While, as a mathematical construct, such an expanse obviously depends on the mind that has constructed it, it is nevertheless purported to enjoy mind-independent existence.)