Quantum quandary #1: A quantum eraser and backward-in-time causation

The experiment of Englert, Scully, and Walther

In a previous letter I mentioned an experiment proposed by Marlan O. Scully, Berthold-Georg Englert, and Herbert Walther. It is a souped-up version of the two-slit experiment with electrons, which in a Physics World poll conducted in 2002 was voted “the most beautiful experiment in physics,” and which according to Richard Feynman “has in it the heart of quantum mechanics” and is “impossible, absolutely impossible, to explain in any classical way.” In this experiment, electrons are launched in front of a plate containing two slits, and electrons are detected on a screen behind the slit plate. If the electron gun in front of the plate is the only source of electrons, and if no electrons are detected behind the plate if the two slits are closed, then common sense dictates that each electron that is detected behind the plate must have passed through either the left slit or the right slit.

If electron counters are placed across the screen, and if we calculate the probability with which an electron will be detected (as a function of the position of the counter), we obtain two distinct probability distributions, one conditional on the assumption that it is possible to find out through which slit each electron went, and one conditional on the assumption that this possibility does not exist.

Figure 1: The solid curve shows how the probability of detection varies across the screen if it is possible to find out through which slit each electron has passed. The dotted curves represent the probability distributions for electrons that went through the left or right slit, respectively.

Figure 2: This curve shows how the probability of detection varies across the screen if it is impossible to find out through which slit each electron has passed.

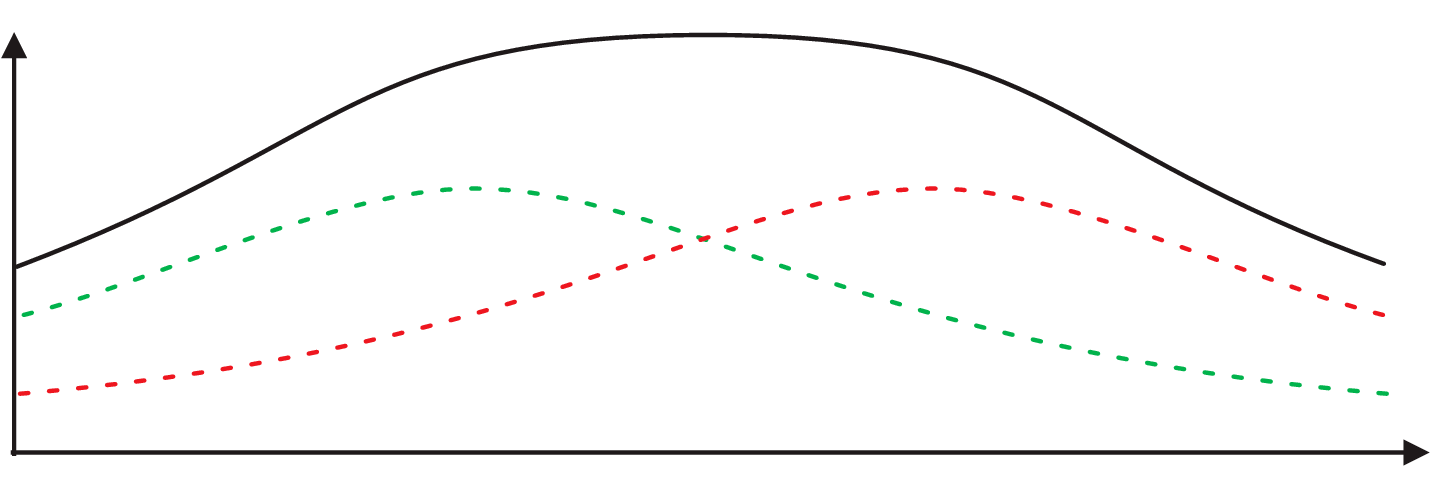
The minimum takeaway here appears to be that if it is impossible to find out through which slit the detected electron has passed, then it is wrong to assume that the electron has passed through a particular slit. For if it is known (or if we simply assume) that the electron has passed through a particular slit, quantum mechanics predicts the solid curve in Figure 1, while what is actually observed is the weird curve in Figure 2. (I say “appears” in deference to a quasi religious community whose members hold that each electron nevertheless always goes through a particular slit.)

Following its discussion in a Scientific American article by Englert, Scully, and Walther in 1994, the experiment originally proposed in 1991 by Scully, Englert, and Walther caused quite a stir. In this experiment the electrons are replaced by Cesium-133 atoms, and a pair of microwave resonance cavities is placed in front of the slits. All atoms are launched in the same excited state. The cavities are tuned to the energy difference dE between this state and the atoms’ ground state, and the design of the cavities ensures that each atom is certain to exit in its ground state. This means that a photon of energy dE is certain to be found inside the cavity through which the atom went.

Figure 3: Schematic of the experiment of Englert, Scully, and Walther.

The two cavities are separated from each other by a pair of electro-optical shutters, which are initially closed. As long as they remain closed, we can find out through which slit the atom went. We only have to check which cavity contains the photon. Thus we can divide the atoms in two groups: if the photon is found in the left cavity, the atom belongs to the “left” group, and if we determine the slit from which the atom emerged, we find that it emerged from the left slit. Likewise, if the photon is found in the right cavity, the atom belongs to the “right” group, and if we determine the slit from which the atom emerged, we find that it emerged from the right slit. Assuming that each atom leaves a mark on the screen where it is detected, we can predict that the marks will be distributed as shown in Figure 1. If we color the marks—green for atoms that deposited a photon in the left cavity, red for atoms that deposited a photon in the right cavity—then Figure 1 looks like this:

Figure 4

If, after an atom has left its mark on the screen, we open the shutters separating the two cavities, it will no longer be possible to determine the slit taken by the atom. How will the marks be distributed in this case? Since we open the shutters after the atom has left its mark on the screen, opening the shutters cannot affect the overall distribution of marks. This will therefore be the same as that in Figure 4, except that we are no longer in a position to divide the marks into a green and a red group.

It is frequently said that by opening the shutters “which-way information” is erased. Some even refer to experimental setups of this kind as quantum erasers. This phraseology is misleading. A measurement in quantum mechanics does not provide information about an already existing state of affairs. In a quite literal sense, it creates the state of affairs the existence of which it indicates. Heisenberg once expressed this by saying that “Die ‘Bahn’ entsteht erst dadurch, dass wir sie beobachten”—the path (of a particle) only comes into being because we observe it. If the possibility of determining the slit taken by the atom no longer exists, what may be said to have been “erased” is only the possibility of obtaining which-way information—information that no one ever obtained.

It is also customary to say, in another misleading phraseology, that the possibility of obtaining which-way information destroys the interference responsible for the pattern of maxima and minima seen in Figure 2. While classical physics makes it possible to attribute such patterns to a physical process called “interference,” in quantum physics what is responsible for these maxima and minima is the rules it provides for calculating statistical distributions (like the above distributions of marks on a screen). It is also customary to say that interference can be “restored,” which simply means that a further modification of the setup makes it possible to observe the pattern of maxima and minima that is observed in the absence of the cavities.

Here is how. Note the photosensor located between the shutters in Figure 3. When the shutters are opened, quantum mechanics predicts that it will detect the photon in half of the cases; the odds for the sensor to respond are fifty-fifty. We thus have another way of coloring the marks on the screen, say, orange if the photosensor responds, and blue if it does not respond. Quantum mechanics further predicts that the orange marks will be distributed exactly like those made by the electrons in Figure 2, and that the distribution of the blue marks will be complementary to that of the orange marks. This means that it will have maxima where the latter has minima and vice versa, and that the sum of the orange and blue distributions will be the same as the sum of the green and red distributions. Interference has been “restored” in the sense that it is separately displayed by each distribution:

Figure 5

We may say that the “green” atoms (i.e., those belonging to the green distribution) went through the left slit, and we may say that the “red” atoms went through the right slit. But how did the “orange” and “blue” atoms pass the slit plate? We cannot say that they went through the left slit, nor can we say that they went through the right slit, for if they did, these patterns of maxima and minima would not be observed. What we can say is that each went through both slits, if only in in the sense that each went through the undivided union of the slits. The distinction we make between the left slit (or cavity) and the right slit (or cavity) does not seem to exist where the atom is concerned.

In addition to saying that the orange or blue atoms went through both slits, we must differentiate between their respective ways of going through both slits. We can distinguish these ways mathematically, by the manner in which the orange and blue distributions are calculated but, other than that, saying that the atoms went through the slits “in the orange way” or “in the blue way” is as good a description as any of their respective behaviors.

And now for the argument for backward-in-time causation. If the experimenters determine the cavity containing the photon, they learn through which slit the atom went. If they open the shutters and determine whether or not the photosensor responds, they learn how the atom went through both slits—in the orange way or in the blue way. They cannot make the atom go through the left slit or through the right slit, yet by doing the former experiment, they can make sure that it went through a particular slit. They cannot make the atom go through the slits in the orange way or in the blue way, yet by doing the latter experiment they can make sure that it went through both slits. And they can choose which kind of experiment to perform after the atom has left its mark on the screen. It follows that their choice contributes to determine what they atom did in its past, as the following diagram illustrates:

Figure 6 [Diagram by Manu Jaiswal]

Some final remarks. Nothing like the back-in-time action with its vicious logic-loops (known from certain Sci-Fi stories) is implied. Because the properties or behaviors of quantum systems depend to some extent on the experimental condition in which they are observed, the behavior of a quantum system at an earlier time can depend on a measurement made at a later time, and thus also on a choice made at a later time. The world has exactly one history. This cannot be changed. But the state of the world at an earlier time can to a certain extent depend on a choice made at a later time.

It would, however, be completely wrong to think that the photon was found in the left cavity—assuming that it was—because the atom went through this cavity. That the atom went through the left cavity is a fact only because the photon was found in the left cavity. The counterfactual argument that the photon could not have been found in the left cavity if the atom had not passed through the left cavity, while logically correct, belongs to the classical universe of discourse. In the quantum domain, arguments involving counterfactual statements sooner or later lead you down the garden path.