“Our modern atoms, the ultimate particles, must no longer be regarded as identifiable individuals. This is a stronger deviation from the original idea of an atom than anybody had ever contemplated. We must be prepared for anything,” Erwin Schrödinger wrote in a slim volume first published in 1951.1
Schrödinger’s caveat notwithstanding, when particle physicists nowadays reflect on the motives for their research, they regularly claim — especially on TV, in press releases, and in grant applications — that their aim is to discover the elementary building blocks of the universe and the forces acting between them. In doing so they present a severe case of cognitive dissonance, inasmuch as this elementary-building-blocks approach to the universe is way past its expiration date.
In the same volume, immediately after giving a couple of examples “of the very direct way in which the old hypothesis of the particle structure of matter has been confirmed far beyond the keenest expectation of previous centuries,” Schrödinger adds:
Still less expected is the modification which our ideas about the nature of all these particles underwent during the same time. … It seems almost ludicrous that precisely in the same years or decades which let us succeed in tracing single, individual atoms and particles, and that in various ways, we have yet been compelled to dismiss the idea that such a particle is an individual entity which in principle retains its “sameness” for ever. Quite the contrary, we are now obliged to assert that the ultimate constituents of matter have no “sameness” at all. When you observe a particle of a certain type, say an electron, now and here, this is to be regarded in principle as an isolated event. Even if you do observe a similar particle a very short time later at a spot very near to the first, ... there is no true, unambiguous meaning in the assertion that it is the same particle you have observed in the two cases. The circumstances may be such that they render it highly convenient and desirable to express oneself so, but it is only an abbreviation of speech; for there are other cases where the “sameness” becomes entirely meaningless; and there is no sharp boundary, no clear-cut distinction between them, there is a gradual transition over intermediate cases. And I beg to emphasize this and I beg you to believe it: It is not a question of our being able to ascertain the identity in some instances and not being able to do so in others. It is beyond doubt that the question of “sameness,” of identity, really and truly has no meaning.
Ten pages further, Schrödinger returns to the question of identity:
If I observe a particle here and now, and observe a similar one a moment later at a place very near the former place, not only cannot I be sure whether it is “the same,” but this statement has no absolute meaning. This seems to be absurd. For we are so used to thinking that at every moment between the two observations the first particle must have been somewhere, it must have followed a path, whether we know it or not. … In other words we assume — following a habit of thought that applies to palpable objects — that we could have kept our particle under continuous observation, thereby ascertaining its identity. This habit of thought we must dismiss. We must not admit the possibility of continuous observation. Observations are to be regarded as discrete, disconnected events. Between them there are gaps which we cannot fill in. There are cases where we should upset everything if we admitted the possibility of continuous observation. That is why I said it is better to regard a particle not as a permanent entity but as an instantaneous event. Sometimes these events form chains that give the illusion of permanent beings — but only in particular circumstances and only for an extremely short period of time in every single case.
The following image — of particle tracks formed in a bubble chamber — exemplifies the particular circumstances in which instantaneous events form chains that give the illusion of permanent beings (for an extremely short time).

We are all primed to think that the strings of bubbles forming in the superheated liquid hydrogen are caused by particles tracing well-defined paths in space. But this is plain wrong. There is a difference between the vapor trail of an airplane in the sky and a particle track in a cloud chamber. (A cloud chamber contains supersaturated vapor of water or alcohol in which the passage of particles is said — in the same faulty phraseology — to cause the formation of strings of droplets.) The airplane causing the vapor trail can be seen, the particle causing a string of droplets is an inference that “should upset everything” if we were to admit it.
But if no particle causes the formation of bubbles in bubble chambers or droplets in cloud chambers, what does? The definite answer to this question was provided by Ole Ulfbeck and Aage Bohr, one of the sons of Niels Bohr. (Both Niels and Aage were awarded a Nobel price in physics, the father in 1922, the son in 1975.) In the title of their 2001 paper,2 Ulfbeck and Bohr posed the following question: “Where Did That Click Come From?” And in the paper they gave the following answer: “It comes by itself, out of the blue!”
Like Kant and subsequently Niels Bohr, Ulfbeck and (Aage) Bohr view space and time as “a scene established for the ordering of experiences.” Clicks given off by counters belong to this scene. Particles travelling from a source to a counter and producing clicks do not: “the connection between source and counter is inherently non-local,” i.e., not mediated by any continuous physical process like the movement of a particle or the propagation of a wave. While clicks are “events in spacetime, belonging to the world of experience,” there are no particles “on the spacetime scene.” The individual click is “an event entirely beyond law.” Genuinely fortuitous clicks, occurring by themselves, form “the basic material that quantum mechanics deals with.”
The click of a detector may be the most basic kind of outcome-indicating event, but it is only one kind of genuinely fortuitous event. Every measurement is genuinely fortuitous not merely with regard to its outcome but more fundamentally with regard to its occurrence. While quantum-mechanical probability assignments are made on the assumption of a successful outcome — this is why the probabilities of the possible outcomes add up to 1 (or 100%) — nothing guarantees the success of an attempted measurement. The redundancy typically built into measuring devices can maximize the likelihood of success, but it cannot guarantee success. Our inability of explaining how it is that measurements have outcomes is known by various unflattering names, such as “the disaster of objectification”3 or “the great scandal of physics”.4
As a student of quantum mechanics, one is primed to think of a measurement as establishing the possession, by a given physical object, of one of a set of alternative properties. More specifically, one is primed to think of a position measurement as establishing the possession, by a given particle or atom, of one of several possible positions, which are defined by macroscopic position-indicators — bubbles in a bubble chamber, droplets in a cloud chamber, blackened grains in a photographic emulsion, and so on. The question at issue thus takes the following form: how are quantum objects given?
To find out, suppose that we perform a series of position measurements, and that each measurement yields exactly one outcome — each time exactly one counter clicks. This can be construed as evidence of (i) a persistent object — not an object that causes clicks but an object whose successive positions are indicated by the clicks — and (ii) a conservation law, the conserved quantity being the number N of simultaneous clicks (in this case, N = 1). This demonstrates the crucial connection between persistent objects and conservation laws.
In the real world there is no conservation law for simultaneous clicks, but there are conservation laws for electric charge, baryon number, lepton number, and several other quantities. In relativistic quantum theory, any set of particles can convert into any other set of particles as long as each of the conserved quantities associated with the initial set of particles equals that associated with the final set of particles. The left side of the following picture illustrates the conversion of a neutron (a bound state of two d quarks and one u quark) into a proton (a bound state of two u quarks and one d quark). The right side illustrates the reverse process.
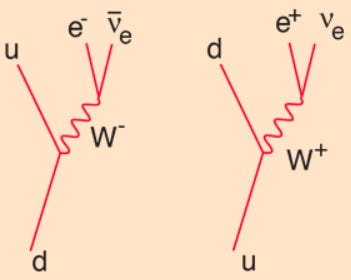
The u quark carries an electric charge q = +2/3, while the d quark has q = -1/3. Each quark has a baryon number B = 1/3. So the neutron has B = 1 and q = 0, while the proton has B = 1 and q = +1. The W boson (which has B = 0) carries away the charge difference between the proton and the neutron. When the negative W converts into an electron (lepton number L = +1) and an anti-neutrino (L = -1, q =0), the electron keeps the negative charge, and when the positive W converts into a positron (L = -1) and a neutrino (L = +1, q = 0), the positron keeps the positive charge.
So much for the vertices at which particle tracks meet — or begin (if a neutral particle converts into two or more charged particles) or end (if charged particles convert into one or more neutral particles). To account for the tracks themselves, one must treat the bubbles in a bubble chamber photograph (or the position-indicators in other records of particle tracks) as the outcome of a single measurements with a gazillion possible outcomes, we must methodically estimate the probability of an outcome containing tracks, and we must compare the same with the probability of an outcome in which no tracks have formed. These probabilities depend on the statistical correlations between the possible position-indicating events, and these correlations depend on the average distance D between those events and on the sharpness of the positions indicated. Particle detectors are designed so that D is sufficiently large while the indicated positions are rather poorly defined by quantum standards. Under these conditions the conservation laws for energy and momentum ensure that the probability of an outcome containing tracks is larger by an enormous factor than the probability of an outcome in which no tracks are seen.
Pay attention to the nature of this quantum-mechanical account. Quantum mechanics never refers to a physical mechanism or a natural process to explain how something comes about. All it gives us is probabilities. In the present case it gives us the result that, under the circumstances considered, observing tracks is overwhelmingly more likely than not observing tracks. So we observe tracks.
To the best of my knowledge, the most comprehensive inquiry into what physicists mean (or ought to mean) when they talk of particles was conducted by Brigitte Falkenburg.5 What she found was that the modern concept of a particle is a veritable hotchpotch of three disparate aspects. The axiomatic aspect covers particle types and their possible interconversions. The operational aspect involves quantum mechanics (as a calculus of correlations) as well as classical measurement laws. The referential aspect concerns the experimental contexts by which individual particles are observed.
As an example of how physicists draw on these disunified aspects, consider the manner in which they deal with scattering experiments. (In contemporary particle physics, such experiments are front and center.) Every scattering experiment begins with either a single particle beam aimed at a fixed target or two intersecting beams. Because the incoming particles are usually accelerated by making them pass through strong magnetic and/or electric fields over large distances, the laws of classical mechanics and electrodynamics are used to describe the creation of particles of definite momentum p. What happens next is described in quantum-mechanical terms. The particles are said to be prepared in a momentum state, and the corresponding mathematical picture of an incoming plane wave of wavelength λ = h/p is used.6 If the target is, say, a crystal, its structure (to be determined) is treated as belonging to the classical boundary conditions of the experiment being conducted, and the incoming plane wave is treated like a classical wave which gets diffracted by the target. After the scattering, either interference patterns or particle tracks are observed, depending on whether one is interested in the structure of the target or the frequencies with which specific sets of particles are produced. To analyze the observed patterns of clicks or to identify the type of particle that goes with a given track, one reverts to purely classical measurement methods. The underlying pragmatic “philosophy” has been summed up by Wolfgang Ketterle in a popular talk, in which he said that after several years of practice one gets used to “preparing waves and detecting particles.”
Among the disunified aspects of the modern particle concept, the referential one is of special interest. The contextuality of properties was brought to light by Niels Bohr. (As you may recall from previous mailings, it consists in the fact that the properties of quantum objects are defined by the experimental contexts in which they are observed, and the fact that they only exist if they are actually observed.) The contextuality of the quantum objects themselves was brought into focus by Brigitte Falkenburg, who stressed that “only the experimental context (and our ways of conceiving of it in classical terms) makes it possible to talk in a sloppy way of quantum objects” [p. 205]:
Quantum theory alone does not admit of constructing objects in the sense of individual spatio-temporal systems with position and temporal duration. Abstracting particle properties such as mass, charge, or spin from their experimental or environmental context means dispensing with spatio-temporal objects and keeping nothing but bundles of dynamic properties of the respective kinds. ... Bare quantum “objects” ... seem to be Lockean empirical substances, that is, collections of empirical properties which constantly go together. However, they are only individuated by the experimental apparatus in which they are measured or the concrete quantum phenomenon to which they belong. [pp. 205‒206]
While, traditionally, Lockean substances are (as Locke himself put it) “such combinations of simple ideas as are, by experience and observation of men’s senses, taken notice of to exist together,” those bundles of dynamical properties need more than the “experience and observation of men’s senses” in order to be “taken notice of to exist together.” They need an experimental context: “The carrier of these properties is nothing but the quantum phenomenon itself, say, a particle track on a bubble chamber photograph7 or the interference pattern of the double slit experiment” [p. 200].
Let us recall from an earlier mailing what this entails. As long as human experience was the only context of empirical science (as it was until quantum theory came along), the elision of the subject — Schrödinger called it objectivation — could be achieved: one could think and behave as if the objective world existed independently of perceiving and thinking subjects who constructed it. But if atoms and subatomic particles owe their properties to the experimental contexts in which they are observed, the experimental apparatus cannot owe its properties to the quantum-mechanical systems of which it is commonly said to be composed. As a result, neither microscopic objects (like atoms and subatomic particles) nor macroscopic objects (like the experimental apparatus) can be thought of as independently existing substances. And this means that the elision of the subject has become impossible.
Falkenburg rightly concludes that subatomic reality is a top-down construct: “The opposite bottom-up explanation of the classical macroscopic world in terms of electrons, light quanta, quarks, and some other particles remains an empty promise” [p. 339]. Subatomic reality dangles top-down from the world of macroscopic objects, which (for the reasons just mentioned) cannot be detached from the experiencing subjects who constructed it.
Science and Humanism, in E. Schrödinger, Nature and the Greeks and Science and Humanism, pp. 103‒171 (Canto Classics, 2014).
O. Ulfbeck and A. Bohr, Genuine Fortuitousness. Where Did That Click Come From? Foundations of Physics 31, 757‒774 (2001).
B.C. van Fraassen, The problem of measurement in quantum mechanics, in Symposium on the Foundations of Modern Physics, edited by P. Lahti and P. Mittelstaedt, pp. 497‒503 (World Scientific, 1990).
D. Wallace, Philosophy of Quantum Mechanics, in The Ashgate Companion to Contemporary Philosophy of Physics, edited by D. Rickles, pp. 16‒98 (Ashgate, 2008).
B. Falkenburg, Particle Metaphysics: A Critical Account of Subatomic Reality (Springer, 2007).
As the “particle property” E (for energy) corresponds to the “wave property” f (for frequency), via E = hf which can also be written in the form E = h/T where T is the duration of a period, so the “particle property” p (for momentum) corresponds to the “wave property” λ, via p = h/λ where λ is the length of a period.
In this connection it is worth noting that in order to identify the type to which a particle belongs, one has to analyze the geometrical properties of its track.


