Demythifying classical physics

Physicists are, at bottom, a naïve breed, forever trying to come to terms with the world out there by methods which involve in essence the same element of direct contact as a well-placed kick.

Those physicists and philosophers of science who wish to take mind (or consciousness, or experience) out of the equation, are hard pressed today to come up with something to which mind-independent existence can be attributed. If individual substances do not qualify, as I have argued in my previous mailing, what does? Not the reification of some calculational tool or tools, as I have argued earlier. While this worked in classical (i.e., pre-quantum) physics, when quantum physics came along it became clear that the reification of calculational tools has never been more than a sleight-of-hand. When I recently pointed this out elsewhere, someone responded by writing:

I can see that Maxwell’s equations, which describe electromagnetic fields, are just another clever calculation device. But does it follow that the electromagnetic fields themselves are just a clever calculation device? If so, what is it that actually carries radio signals, shields the earth from solar flares and so on?

Whichever the context (classical or quantum), what we have for sure is correlations. In the so-called classical limit, in which quantum physics degenerates into classical physics, the statistical correlations of quantum physics turn into determinative correlations, meaning that they enable us to make exact predictions: if we jiggle the electrons here, in this antenna, in some particular way, we can predict how the electrons over there, in that antenna, will jiggle as a result. This seemed to make it possible to think of the electromagnetic field as a physical entity in its own right, which — instead of just being a device for calculating the effects that charges have on charges — mediates the action of charges on charges.

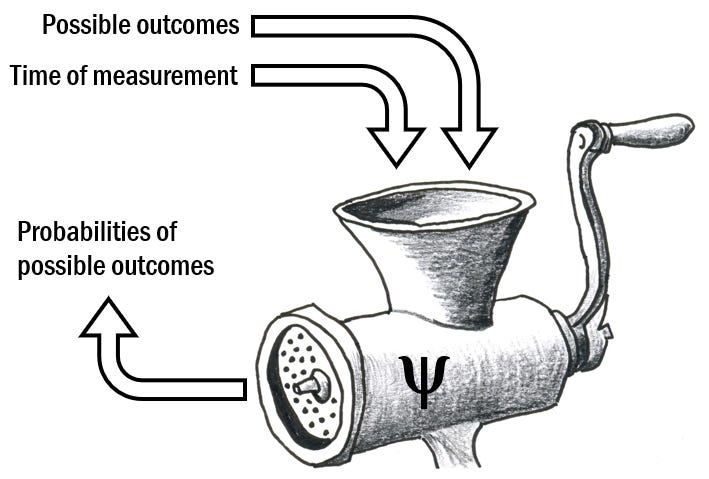
What also happens in the classical limit is that quantum states degenerate into classical states. A classical state (i.e., the state of a classical physical system) is what everybody understands by “the state of a physical system,” to wit: a bundle of possessed properties. A quantum state (i.e., the state of a quantum-physical system) is what nobody outside the physics community understands by “the state of a physical system,” to wit: a probability algorithm. A probability algorithm is a computing machine with inputs and outputs. In the case at hand you specify a measurement by inserting its possible outcomes along with the time of measurement, and out pop the probabilities of the possible outcomes:

A quantum grinder

What also happens, as a result, is that instead of statistical correlations between outcome-indicating events we now have determinative correlations between classical states, and such correlations can be thought of in causal terms, as relations between causes and effects. What does not happen in the classical limit is that the quantum-mechanical correlations turn into physical mechanisms or natural processes by which causes produce their effects. Thinking of the classical electromagnetic field as a physical entity that mediates the action of charges on charges is inconsistent with the quantum-mechanical origin of the classical laws.

The classical electromagnetic field at a point x in space and a moment t in time is not something that exists at that point and at that moment. It is another mathematical machine with inputs and outputs. I’ll put it to you without using the philosophically unhelpful concept of force: you insert (i) the charge of an electrically charged particle and (ii) a tiny segment of a spacetime path at or near a point x and a moment t, and out pops the change that the particle’s momentum undergoes as it travels along that tiny path segment. The classical electromagnetic field determines the extent to which a charged particle’s motion changes at or near a point of spacetime, but it does not cause this change. The change is caused by the distribution and motion of charged particles elsewhere.

Take the shielding of the Earth from the solar wind — the constant stream of particles expelled by the Sun’s corona. The charged particles whose distribution and motion deflect the solar wind is to be found in Earth’s outer core. Heat from the solid inner core drives convection currents in the electrically conducting fluid outer core, and these are organized into vortices by the Coriolis effect. The Earth’s magnetic field is the result of a feedback loop: in the presence of the field, the motion of the electrically conducting fluid (caused by the Earth’s rotation and the Coriolis effect) induces electric currents, which generate and sustain the Earth’s magnetic field.

Why does it sound odd to say that it is electric currents in the Earth’s outer core that deflect the bulk of the solar wind towards the Earth’s poles, preventing it from reaching the Earth’s surface? The answer is contained — like a pearl in an oyster — in the first two paragraphs of a paper¹ written in the early 1970s by Bryce DeWitt and Neill Graham (I’ve emphasized the pearl):

No development of modern science has had a more profound impact on human thinking than the advent of quantum theory and the discovery of the laws of quantum mechanics. Wrenched out of centuries-old thought patterns, physicists of a generation ago found themselves compelled to embrace a new metaphysics. The distress which this reorientation caused continues to the present day. Basically, physicists have suffered a severe loss: their hold on reality.

Philosophers have been quick to step in with assurances that the problem is only in the mind, and that if physicists would just adopt the right epistemological stance, all difficulties would disappear. But physicists are, at bottom, a naïve breed, forever trying to come to terms with the "world out there" by methods which, however imaginative and refined, involve in essence the same element of direct contact as a well-placed kick. The reality of direct contact imparts a view of nature which no metaphysical arguments, however ingenious, can erase.

In Quantum quandary #2 I raised the question of how it was possible to predict such quantities as the outcome of a measurement of X(C) on the basis of measurements of Y(A) and Y(B), regardless of the order in which the three measurements are made, and regardless of the distances between the three particles involved. There are two possible explanations. The first is that the three particles are created in a state that predetermines the outcome of each of the six possible measurements. This explanation is ruled out by the absence of (non-contextual²) pre-existent values. The second possible explanation is that the outcomes of a pair of Y measurements somehow influence the outcome of the only compatible X measurement — instantaneously and at any distance. This explanation is ruled out by the theory of relativity. In sum: no viable solution to this and numerous other quantum quandaries has ever been found.

Discussing classical electromagnetism in terms that are consistent with its quantum-mechanical origin brings us face to face with our naiveté, which is by no means confined to physicists. I know of only one historical figure, the Serbo-Croatian polymath Roger Boscovich, who stressed that action by direct contact, while easy to apprehend viscerally, is even harder to understand theoretically than action at a distance. (Action by direct contact is readily understood only if one does not inquire how it actually works. How, if you please, does the electromagnetic field act on a charge, in physical rather than purely mathematical terms?) Boscovich formulated an atomic theory in which matter is reduced to a dynamic system of relations between dimensionless points lacking mass and substantiality. He accounted for the stability of material objects in terms of equilibria between attractions and repulsions, much like quantum theory does today. So impressed was Friedrich Nietzsche by his elimination of matter that he compared him to Copernicus, writing that³

while Copernicus convinced us to believe, contrary to all our senses, that the earth does not stand still, Boscovich taught us to renounce belief in the last bit of earth that did “stand still,” the belief in “matter,” in the “material,” in the residual piece of earth and clump of an atom: it was the greatest triumph over the senses that the world had ever known.

I still remember my puzzlement when learning that the tides act like brakes on Earth’s rotation, and that the angular momentum lost by the rotating Earth as a result is picked up by the Moon, causing it to slowly spiral outwards, away from the Earth. How does angular momentum get transferred from the Earth to the Moon? Just so Newton’s contemporaries must have wondered at his theory of gravity. Newton’s stance in this respect is well known⁴:

I have not been able to discover the cause of those properties of gravity from phænomena, and I frame no hypotheses. …To us it is enough, that gravity does really exist, and act according to the laws which we have explained, and abundantly serves to account for all the motions of the celestial bodies, and of our sea.

For Newton’s contemporaries, the difficulty of accounting for gravity’s action at a distance appeared to arise from the fact that gravitational effects were simultaneous with their causes. In the 20th Century, the delay between causes and effects in relativistic theories made it seem possible to explain “how Nature does it.” In actual fact, the opposite is the case. The structure of relativistic spacetime makes redundant the postulation of a physical process by which electromagnetic or gravitational causes produce their effects.

To see this, consider two events e1 and e2, the first happening at a place marked x1 and a time marked t1, the second happening at x2 and t2, and suppose that e1 is the cause of e2. Why is it that e2 happens at t2, rather than at any other time (relative to t1)? There are two possible reasons: the causal relation could be mediated, or it could be unmediated. In the mediated case, t2 is determined by the speed of mediation. This would be either the speed of a material object traveling from x1 to x2 or the speed of a wave propagating in an elastic medium. In the unmediated case, t2 can only depend on the invariant speed.

In every physical theory that satisfies a principle of relativity, such a speed exists. In theories that satisfy the Galilean principle of relativity, it is infinite. Whatever travels with an infinite speed (i.e., whatever takes not time to get from here to there), as described in terms of one inertial coordinate frame, does so also when described in terms of another inertial frame. In theories that satisfy Einstein’s principle of relativity, the invariant speed is finite. It is then called the “speed of light” (in vacuum). If something were to travel with this speed relative to one inertial coordinate frame, it would do so relative to any other inertial frame.⁵

So if the causal relation between e1 and e2 is unmediated, then in the Galilean (“non-relativistic”) case t2 must be equal to t1, and in the Einsteinian (“relativistic”) case it must be greater than t1 by just the amount of time it would take an object to travel from x1 to x2 at the finite invariant speed, never mind that if the causal relation is unmediated then nothing actually travels from x1 to x2. What accounts for the delay in relativistic causation is not something that travels from x1 to x2 but the structure of relativistic spacetime.

Returning to the mysterious transfer of angular momentum from the Earth to the Moon, physicists are usually perfectly happy to “explain” this by invoking the conservation of angular momentum. If the Earth and the Moon are considered as a closed physical system, the Earth’s loss must be the Moon’s gain. Whence, then, our confidence in the validity of conservation laws? What we need to understand here is that distances and durations are not built into space and time. It is we who decide how distances and durations are measured, and in this we are guided by convenience. As was stressed by Henri Poincaré,⁶ “one geometry cannot be more true than another, it can only be more convenient.” Which geometry, then, is the most convenient? It is that which yields the mathematically simplest formulation of the laws of physics. In the absence of gravity, it is the Minkowski geometry of spacetime; in the presence of gravity, it is a pseudo-Riemannian geometry.

It is the principle of relativity (cf. Footnote 5) that takes us further. It implies that if ℱ is an inertial frame, then so is any coordinate frame that, relative to ℱ, (a) is shifted in space by a given distance in a given direction, (b) is shifted in time by a given amount of time, (c) is rotated by a given angle about a given axis, or (d) moves with a constant speed in a constant direction. What the principle of relativity buys us is that the total linear momentum, the total energy, and the total angular momentum of a closed physical system are conserved. The first follows from (a), the second from (b), and the third from (c). To cut a long story short, the existence of these conserved quantities is a consequence of a convenient choice that we have made.

What about item (d)? In non-relativistic physics, where simultaneity does not depend on which inertial frame is chosen to describe the physical goings-on, energy (like any other conserved quantity) can disappear in one place and simultaneously reappear in another place, without violating the law of energy conservation. In relativistic physics, this cannot happen. If energy were to disappear in one place and simultaneously reappear in another in terms of one inertial frame, there would be other inertial frames (moving at a constant speed relative to the former) in terms of which the energy would reappear at later time, and yet others in terms of which the energy would reappear at an earlier time! In relativistic physics, therefore, energy must be locally conserved. This can be stated as an equation of continuity, which says that during any given interval of time, the amount of energy that crosses the boundary of a region R of space must be equal to the amount by which the energy contained in R increases or decreases.

If this tempts us to think of energy (or any other conserved quantity) as some fluid stuff sloshing about space, we need to re-consider the quantum-mechanical origin of the classical laws. At their origin are the laws which govern particle collision experiments. These laws ensure (among other things) that the total energy-momentum⁷ of the incoming particles equals the total energy-momentum of the outgoing particles. Whatever happens between the creation of the incoming particles and the detection of the outgoing particles is treated as a black box. Whatever happens between the emission of a radio signal and its reception must therefore be treated as a black box as well, not least because, as Feynman said at the beginning of his brilliant Caltech lectures,⁸ “philosophically we are completely wrong with the approximate law” (the emphasis is his own). Imagining fields that behave like spring mattresses when you bounce up and down on them can be useful, even indispensable, for engineering purposes, but it can have nothing to do with what really happens or is the case.

In this regard the situation in physics is similar to that in neuroscience or the philosophy of mind. Whether we consider the brains studied by neuroscience as part of the world of experience or as independently existing material objects, they cannot account for the fact that we have experiences. As Friedrich Lange put it one and a half centuries ago,⁹

we must never forget that … the brain and all the structures which we may yet discover there as causes of thought, are only ideas, which indeed form a self-coherent world, yet a world which points to something beyond itself.

In quantum mechanics we have correlations between measurement outcomes or property-indicating events, and there are three ways to deal with them. The philosophically most barren approach is instrumentalism, which reifies outcome-indicating devices. The most cockamamie and ineffectual approach is Ψ-ontology,¹⁰ which reifies quantum states and consequently fails to explain how measurements can have outcomes — a state of affairs that has been dubbed “the disaster of objectification.” The third approach is to relinquish the distinction between observations qua experiences and observations qua property-indicating facts or events. It takes seriously the truism that no property can be indicated in the absence of a sentient being to whom it is indicated. The problem then is not objectification (getting measurement outcomes from reified quantum states) but what Schrödinger has called objectivation (constructing an objective world from experiences). The solution to this problem we owe to Kant. It was extended by Niels Bohr to include the property-indicating experiences which quantum mechanics serves to correlate.

Bohr never ventured to explore the ontological implications of the quantum-mechanical correlation laws, insisting instead that “the facts which are revealed to us by the quantum theory ... lie outside the domain of our ordinary forms of perception”¹¹ and therefore elude “the conceptual structure upon which our customary ordering of our sense-impressions depends and our customary use of language is based”.¹² Like the neuroscience of today, Bohr leaves us with a set of ideas to which Lange’s words again apply: they “form a self-coherent world, yet a world which points to something beyond itself.”

What this “something beyond itself” may be, I will discuss in future mailings. Suffice it to say that neither instrumentalism nor Ψ-ontology make it possible to ferret it out.

1. B. S. DeWitt and R. N. Graham, Resource Letter IQM-l on the Interpretation of Quantum Mechanics, American Journal of Physics 39, 724-738 (1971).

2. See my previous mailing.

3. F.W. Nietzsche, Beyond Good and Evil, p. 14 (Cambridge University Press, 2002).

4. Sir Isaac Newton’s Mathematical Principles of Natural Philosophy and his System of the World, edited by F. Cajori, translated by A. Motte, p. xvii (University of California Press, 1687/1962).

5. (i) The principle of relativity requires that all inertial coordinates frames are “created equal”: the laws of physics do no favor any particular such frame or class of frames. Hence we cannot use physical laws to distinguish one from another.

(ii) A coordinate frame is inertial if and only if the position components x,y,z of any freely moving classical object change by equal amounts Δx, Δy, Δz in equal time intervals Δt.

6. H. Poincaré, Science and Hypothesis, p. 50 (The Walter Scott Publishing Company, 1905).

7. In relativistic theories energy and momentum are welded together as the 1+3 components of a single quantity.

8. R.P. Feynman, R.B. Leighton, and M. Sands, The Feynman Lectures in Physics, Vol. 1 (Addison–Wesley, 1963).

9. F.A. Lange, The History of Materialism and Criticism of its Present Importance, p. iii.224 (Kegan Paul, 1865/1925).

10. The near homonymy with “scientology” is not altogether unintentional.

11. Niels Bohr: Collected Works, Vol. 6, p. 217 (North-Holland, 1985).

12. Niels Bohr: Collected Works, Vol. 10, pp. xxxv-xxxvi (Elsevier. 1999).