Quantum entanglement: No reasonable definition of reality could be expected to permit this.
On the 2022 Nobel Prize in Physics
This year’s Nobel Prize in Physics was awarded jointly to Alain Aspect, John F. Clauser, and Anton Zeilinger for experiments with entangled photons, establishing the violation of Bell inequalities, and pioneering quantum information science.
[T]he early Bell experiments drove the development of what is often referred to as the “Second Quantum Revolution”. Two of this year’s laureates, John Clauser and Alain Aspect, are honoured for work that initiated a new era, opening the eyes of the physics community to the importance of entanglement, and providing techniques for creating, processing and measuring Bell pairs in ever more complex and mind-boggling scenarios. The experimental work of the third Laurate, Anton Zeilinger, stands out for its innovative use of entanglement and Bell pairs, both in curiosity driven fundamental research and in applications such as quantum cryptography.1
So, what is quantum entanglement?
Most simply put, quantum entanglement is a type of correlation between simultaneous random events in different locations, which cannot be accounted for in either of the two explanations that are available to us: direct causation (event A directly increases or decreases the likelihood of event B, or vice versa) or a common cause (an earlier event C influences the respective likelihoods of both A and B). (Recall the introductory remarks to this post regarding a correlation between ice cream consumption and drowning incidents.) The most famous correlations predicted by quantum mechanics are those that were first discussed by Albert Einstein, Boris Podolsky, and Nathan Rosen (EPR) in 1935, and those that were first discussed half a century later by Daniel Greenberger, Michael Horne, and Anton Zeilinger (GHZ). EPR correlations formed the subject of this post, and GHZ correlations were tackled in this post.
In the former post I made use of a setup involving two particles that are “prepared in the singlet state.” Here I must stop at once to clarify the meaning of “state” in quantum mechanics and what it means to “prepare” one. As Scott Aaronson pointed out in the lecture notes to his introductory course on Quantum Information Science,
There’s an extreme point of view in quantum mechanics that unitary transformations are the only thing that really exist, and measurements don’t. And the converse also exists: the view that measurements are the only things that really exist, and unitary transformations don’t.
The former point of view interprets a quantum state as a physical state of some sort, whose evolution (from earlier times to later times) is represented mathematically by a unitary transformation. This point of view “solves” the notorious measurement problem — which is that the process of measurement cannot be described by a unitary transformation — by getting rid of measurements altogether. If this doesn’t strike you as a promising strategy, you could point out that the only way to test quantum mechanics is to perform measurements, and to compare the correlations between their outcomes that are observed with those that are predicted by quantum mechanics. (Spoiler alert: they agree perfectly.) On the latter view, unitary transformations do exist, though not as descriptions of the evolution of physical states. A quantum state is a mathematical tool for assigning probabilities to the possible outcomes of any measurement that may be made at a specified time. It depends on the experimental procedure or procedures (including but not limited to measurements) by which it is said to be “prepared.” Unitary transformations are the mathematical tools by which quantum states pertaining to different times are related to each other.
To resume, each of the two particles prepared in the singlet state enters a device capable of performing one of three measurements, each having two possible outcomes (indicated by the flashing of a red or green light). In each run of the experiment the two measurements are randomly selected. Quantum mechanics predicts that, after a large number of runs, the sequence of red and green lights flashed by either device is completely random. In particular, the two devices flash different colors half of the time. But quantum mechanics also predicts that whenever both devices perform the same measurement, equal colors are never observed. The challenge posed by these correlations is to understand how it is possible for the colors to invariably differ when identical measurements are made, even though the individual sequences of colors are completely random.
Assuming that the observed correlations have a common cause, we end up with a Bell inequality which states that the probability of observing different colors is equal to or greater than 5/9, whereas quantum mechanics predicts that the probability of observing different colors equals 1/2. A common-cause explanation is thereby ruled out, as are instruction sets (properties that are possessed by the particles before they reach the devices, properties whose existence is merely revealed by the measurements), and so are local hidden variables (unobservable properties transmitted continuously from spacetime point to “neighboring” spacetime point). The alternative explanation — instantaneous transmission of information from one device to the other — is ruled out by the theory relativity. In the renowned paper of 1935, which features his eponymous cat, Erwin Schrödinger expressed the view that “[m]easurements on separated systems cannot directly influence each other — that would be magic.” In 1964 Bell showed that the magic was real and inevitable.
What distinguishes the GHZ setup from EPR-type setups is that the latter reveal an inconsistency between classical intuitions and quantum-mechanical predictions at the level of statistics, while the former achieved what many had thought to be impossible: it revealed such an inconsistency through a single event. The GHZ setup (discussed here) made use of three entangled particles. Each particle enters a device capable of performing either of two measurements — call them X and Y — each of which has two possible outcomes (+1 or –1). For this entangled three-particle state, quantum mechanics predicts that
whenever X is performed on each particle, the product of the outcomes will be –1,
whenever X is performed on one particle while Y is performed on the two other particles, the product of the outcomes will be +1.
This allows us to predict for any one particle
what its X value will be if either the X values or the Y values of the two other particles have been measured,
what its Y value will be if the X value of one other particle and the Y value of the remaining particle have been measured.
So how is it possible to make these predictions regardless of the distances separating the three particles? Let’s again try instruction sets (hidden properties that are revealed by measurements). We thus assume the existence of three hidden variables X₁,X₂,X₃ each having the value +1 or –1, each waiting to be revealed by the outcomes of two far-away Y measurements. We also assume three hidden variables Y₁,Y₂,Y₃ each having the value +1 or –1, each waiting to be revealed by the outcomes of a far-away X measurement and a far-away Y measurement. We can therefore conclude that X₁ equals the product of Y₂ and Y₃; that X₂ equals the product of Y₁ and Y₃, and that X₃ equals the product of Y₁ and Y₂. And we can further conclude that the product X₁X₂X₃ equals the product of these three products:
X₁X₂X₃ = (Y₂Y₃) (Y₁Y₃) (Y₁Y₂) = (Y₁Y₁) (Y₂Y₂) (Y₃Y₃) = (Y₁)² (Y₂)² (Y₃)²
But since the Y values are either +1 or –1, and since the squares of both +1 and –1 are equal to +1, assuming hidden variables leads to X₁X₂X₃ = +1, a prediction that can be shown to be false by a single simultaneous measurement of the three X values. Once again, the two possible ways of explaining the quantum mechanical predictions are ruled out, the first by the incompatibility of quantum mechanics with hidden variables, the second by the theory of relativity.
The term “entanglement” was coined by Schrödinger, who wrote2:
When two systems, of which we know the states by their respective representatives, enter into temporary physical interaction due to known forces between them, and when after a time of mutual influence the systems separate again, then they can no longer be described in the same way as before, viz. by endowing each of them with a representative of its own. I would not call that one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought. By the interaction the two representatives [the individual quantum states] have become entangled.
Schrödinger’s language is potentially misleading, inasmuch as the quantum states associated with physical systems are not literally “representatives” by which the systems are “described.” Rather they are “expectation catalogs,” as he called them in his cat paper, i.e., tools for assigning probabilities to possible measurement outcomes. Mathematically speaking, the possible expectation catalogs associated with a two-particle system are members of a vector space which is the direct product V₁⊗V₂ of the vector spaces associated with the individual particles. Most vectors in V₁⊗V₂ cannot be written as a single product of vectors ψ₁⊗ψ₂. In this case it isn’t possible to “endow [each particle] with a representative of its own.” On the other hand, all vectors in V₁⊗V₂ can be written in the form of a sum Σₖ cₖ ψₖ⊗ψₖ with non-negative coefficients cₖ. A two-particle state for which two or more coefficients are positive exhibits entanglement.
The aforementioned singlet state is of the form
Ψ = c ψ₁(↑) ⊗ ψ₂(↓) – c ψ₁(↓) ⊗ ψ₂(↑),
where c equals √½ and ψ₁(↑) tells us that the spin of the first particle is certain to be found parallel to some axis (defined by the measurement apparatus), while ψ₂(↓) tells us that the spin of the second particle is certain to be found antiparallel to the same axis. Correction: ψ₁(↑) would tell us this if it were associated with the first particle, but it isn’t because neither particle is “endowed” with a spin state of its own. And since the axis defined by the measurement apparatus is arbitrary, nothing can be said about either particle’s spin individually, where “nothing” means the same as saying that each individual spin is equally likely to be found up or down. All actionable information provided by Ψ concerns the two-particle system as a whole, in the form of conditional statements such as “if the spin of the first particle is found ‘up’ then the spin of the second particle is certain to be found ‘down’.”
In the penultimate paragraph of their famous paper of 1935, EPR remarked on the apparent dependence of the properties of the second particle on the measurement carried out on the first particle: “No reasonable definition of reality could be expected to permit this.” Duh!
Let’s face it: quantum mechanics allows us to make predictions, but it does nothing by way of explaining how the world works. If there is a physical basis for the certainty of finding the second spin antiparallel to the first, it is the quantum-mechanical correlations, rather than any underlying mechanism or process. If we want an explanation for the correlations, we must ask, what must be the case so that there can be a world such as we experience, a world which seems to be governed by rational laws, a world which appears to be comprehensible, a world which gives the impression of being amenable to causal analysis — up to a point, until it isn’t. Trying to understand the world in terms of the cognitive tools available to us is putting the cart before the horse.
In the quantum domain, anything can happen except what violates a conservation law. When a singlet state comes into being — either through a temporary interaction between two particles or as the result of the decay of a single particle — what comes into being is a state whose total spin is 0. It is because the total spin of an isolated system is conserved that the individual spins, when measured with respect to the same axis, are found pointing in opposite directions. (In their 1935 paper, EPR based their argument on the conservation of momentum instead.)
And it is because anything can happen in the quantum domain that the fundamental theoretical framework of contemporary physics is a calculus of correlations. In principle this calculus serves to assign a probability (conditional on the relevant information) to everything that can happen, and the probability assigned is strictly zero only for events that would violate a conservation law. If then there is one conclusion that can safely be drawn, it is that whatever acts in the world is an infinite agent or force that works under self-imposed constraints. And if there is anything that remains to be figured out, it is why — to what end — it works under the particular constraints that it does.
Although John Bell received many awards, they did not come for many years, until the nature of his exceptional achievements became fully realized. Between 1987 and 1989 he was awarded the Hughes Medal of the Royal Society, the Dirac Medal of the Institute of Physics, and the Heineman Prize of the American Physical Society. In 1988 he received honorary degrees from both the Queen’s University of Belfast and Trinity College, Dublin. He was nominated for a Nobel prize and, had he lived longer, might well have received it. Sadly, John Bell died of a stroke on 1 October 1990, aged 62.
In 1967, the strange title Physics Physique Fizika of the journal in which Bell’s seminal paper appeared caught the eye of a budding experimentalist. While leafing through the first volume, John Clauser noticed Bell’s article, realized that it was important, but at first didn’t believe it. He tried to find a counterexample, tried to disprove it, and eventually realized there was nothing wrong. He then wrote to Bell (as well as to David Bohm and Louis de Broglie) to double-check that he had not overlooked any relevant prior experiments. He hadn’t. In his reply Bell wrote3:
In view of the general success of quantum mechanics, it is very hard for me to doubt the outcome of such experiments. However, I would prefer these experiments, in which the crucial concepts are very directly tested, to have been done and the results on record. Moreover, there is always the slim chance of an unexpected result, which would shake the world!
The thought experiment by which Bell derived his famous inequality, like many of its didactic incarnations, is not suitable for testing. Having derived a more general inequality that could be tested experimentally, Clauser drafted an abstract for a meeting of the American Physical Society proposing a test. As soon as it appeared in print, Clauser received a phone call from Abner Shimony, who said that he and his student Mike Horne had come to the same conclusions. Their own quest for previous experimental evidence had let them to Frank Pipkin at Harvard, whose PhD student Richard Holt was just then setting up the experiment that Clauser had proposed. Clauser, Horne, Shimony, and Holt — henceforth known by their initials CHSH — decided to coauthor a paper, which subsequently served as the bridge between theory and experiment.
The first experimental test of the CHSH inequality was done in 1972, by Clauser and Stuart Freedman, who was awarded his PhD for this work. Much to the disappointment of Clauser, who had hoped for a different outcome, the results provided “strong evidence against local hidden-variable theories”.4 Clauser went on to perform three more experiments testing the foundations of quantum mechanics, with each new experiment confirming and extending his results.

To arrive at their conclusion, Freedman and Clauser had to make certain assumptions.5 Though eminently reasonable, they indicate the existence of “loopholes.” To actually plug the so-called locality loophole, one must make sure that the random choices made by Alice and Bob are independent of each other. Assuming the correctness of the theory of relativity, this amounts to making sure that in the time between the two choices no message traveling at or below the speed of light can be sent by Alice to Bob (or by Bob to Alice).
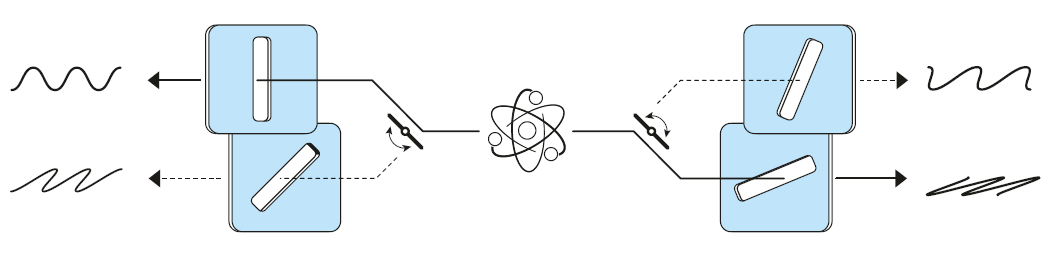
Alain Aspect was the first to design an experiment that avoided the locality loophole. In 1981 and 1982, together with collaborators Phillipe Grangier, Gérard Roger, and Jean Dalibard, Aspect performed a series of experiments using improved techniques and novel instruments. He established a violation of a Bell inequality with very high precision, tens of standard deviations, as compared with the six standard deviations of the Freedman–Clauser experiment. In his third experiment,6 which garnered the most attention, Aspect ensured the independence of Alice and Bob by using polarization settings that changed randomly during the time of flight of the photons between the detectors.
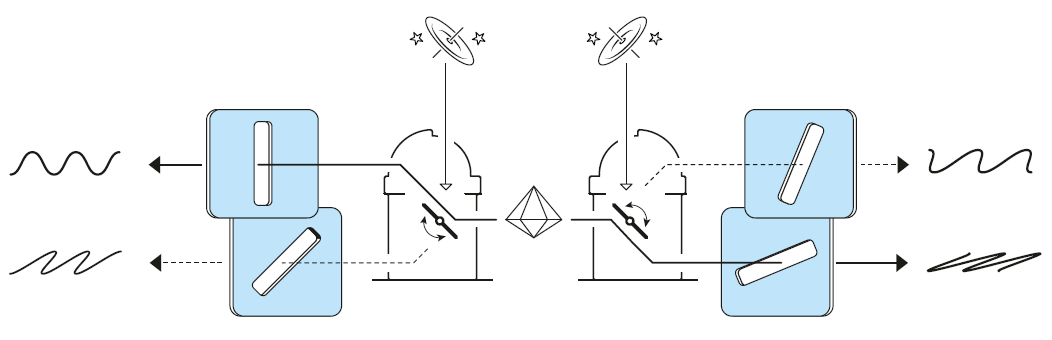
The experiment was not ideal, since the distance between the polarizers was too small to allow for truly random settings between them. It would take more than 15 years before Anton Zeilinger’s group could test the inequality under strict local conditions, with the observers separated by 400 m and with a number of other technical improvements.7
Of the other loopholes, the one considered to be the most important is the detection loophole. This arises because no detector has 100% efficiency — some photons are invariably lost, and these photons might conspire to fake a violation of a Bell inequality. This can be avoided by having sufficiently good photon detectors. The detection loophole was first closed in an experiment using trapped ions8 and later in other systems. However, in these experiments one could not close the locality loophole, and it was only in the years 2015-17 that four groups, one of them led by Zeilinger, managed to simultaneously close both the locality and detection loopholes.
The experiments of Clauser and Aspect opened the eyes of the physics community to the profound importance of entanglement, and they provided the tools to use distant, but still entangled, photons as a quantum resource. This resource has become central to the rapidly developing field of quantum information science.
There is, first of all, the discovery that quantum states can be “teleported” but not “cloned.” The difference is the same as between moving and copying a computer file from one folder to another: in the first instance the quantum state ψ of system A gets obliterated as system B “enters” or “acquires” ψ; in the second instance, if that could happen, the quantum state of system A would remain intact as system B “enters” or “acquires” it. If a quantum state could be cloned once, it could be cloned many times, which means that the unknown quantum state of a single quantum system could be determined with arbitrary precision. (In reality, a quantum state can only be determined, with arbitrary precision, by performing measurements on an ensemble of identically prepared quantum systems.) If a quantum state could be cloned, it would also imply that information could be transferred instantaneously, in violation of the theory of relativity.
An important goal of quantum technology is to communicate quantum information over very large distances. The simplest means is to use an optical fiber, but the problem with this is that light is attenuated; on average every second photon is lost in a 10-kilometre-long fiber. In classical communication networks, the problem is solved by placing amplifiers along the fiber links. But owing to the no-cloning theorem, this is not possible in the quantum case, since classical amplifiers effectively make copies of the original message.
There are two ways to deal with this loss in quantum communication. One is to send signals through space using satellites. This approach was spearheaded by a team lead by Jian-Wei Pan, using the first quantum communication satellite, which was launched by China in 2016. Pan and colleagues demonstrated a satellite-based distribution of entangled photon pairs between two locations separated by 1203 km on Earth, through two satellite-to-ground downlinks with a total length varying from 1600 to 2400 km. Later, in collaboration with Zeilinger’s group, they distributed entanglement between China and Austria using the same satellite. The second approach to long distance quantum communication uses quantum repeaters, which are devices based on entanglement swapping, a phenomenon closely related to quantum-state teleportation.
Controlled entanglement is by no means restricted to polarization states of photons. Enormous effort has gone into establishing other two-level systems that can be used in quantum technology, and in particular in quantum computing. Today, “quantum technology” refers to a very broad range of research and development, encompassing quantum computing, quantum simulation, quantum communication, and quantum metrology and sensing. In all of these areas quantum entanglement plays a central role. The following example demonstrates that violations of Bell inequalities are not “just” a matter of quantum mechanical ontology, but can be put to practical use.
The only known way to send messages that are guaranteed to be safe from eavesdropping is to have a shared and secret cryptographic key that is only used once. The problem is how to distribute a key shared by Alice and Bob in a secure way, and this is where quantum key distribution (QKD) comes in. In 2006 the Zeilinger group used an entanglement-based QKD protocol proposed by Artur Ekert in 1991 and an optical free space link, to establish a secure key between two Canary Islands, La Palma and Tenerife, which are separated by 144 km. In a test of the CHSH inequality using polarization-entangled photon pairs, the experimenters demonstrated violation of the local realistic limit by more than 13 standard deviations.
The Nobel Committee for Physics: Scientific Background on the Nobel Prize in Physics 2022, retrieved via this link.
E. Schrödinger, Discussion of Probability Relations Between Separated Systems, Proceedings of the Cambridge Philosophical Society 31, 555–563 (1935).
J.F. Clauser, Early History of Bell’s Theorem, in R.A. Bertlmann and A. Zeilinger (eds.), Quantum [Un]speakables: From Bell to Quantum Information, pp. 61–98 (Springer, 2002).
S.J. Freedman and J.F. Clauser, Experimental test of local hidden-variable theories, Physical Review Letters 28, 938–941 (1972).
The following material is based on the document referenced in Note 1.
A. Aspect, J. Dalibard and G. Roger, Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers, Physical Review Letters 49, 1804–1807 (1982).
G. Weihs, T. Jennewein, C. Simon, H. Weinfurter and A. Zeilinger, Physical Review Letters 81, 5039–5043 (1998).
M.A. Rowe, D. Kielpinski, V. Meyer, C.A. Sacket, W.M. Itano, C. Monroe and D.J. Wineland, Experimental violation of a Bell's inequality with efficient detection, Nature 409, 791–794 (2001).






Excellent. Wonder if there was any involvement of anyone from the ULL in that test in Tenerife.