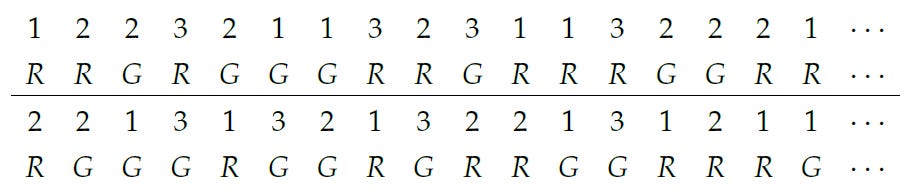Quantum quandary #3: Bell’s theorem

How the hippies made physics great again

There are two ways to account for correlations: direct causation or the existence of a common cause. To appreciate the difference, consider the following anecdote. A large ice cream company had recorded its sales over a period of several years. When its records were compared with a record of drowning incidents during the same period, it was found that whenever the ice cream sales were higher, more people drowned. Direct causation in this case would mean that more people drowned because more ice cream was consumed, or that more ice cream was consumed because more people drowned. The existence of a common cause would mean that a third factor was responsible for both the increase in ice cream consumption and the increase in drowning incidents. The correct answer is obvious: there was a common cause, namely, the weather. On warmer days more ice cream was consumed, more people went swimming, and, consequently, more people drowned. The trouble with quantum mechanics (one of those troubles!) is that the correlations it correctly predicts defy both kinds of explanation. Direct causation would require the instantaneous transmission of signals, which is ruled out by the special theory of relativity, and common-cause explanations are ruled out by Bell’s theorem.

A brief history of Bell’s theorem

This section incorporates information gleaned from David Kaiser’s charming book How the Hippies Saved Physics (Norton, 2011).

The creators of quantum mechanics formed a tight-knit community. They knew each other well, continually crossing paths at Bohr’s institute in Copenhagen, at the University of Göttingen, and at informal conferences in Brussels sponsored by the industrialist Ernest Solvay. When not in the same town, they kept up their conversations by letter, tens of thousands of which have survived. Inventoried, archived, and translated, these letters have been subjected to the kind of scrutiny once reserved for Scripture. They reveal just how earnestly the early quantum physicists worked to make sense of their new formalism, to wrap their heads around how the world could possibly work that way. The same philosophical impulse shaped their earliest pedagogical writings. Not a few textbooks included entire chapters on philosophical problems arising from the new theory.

All that changed after World War II. Now textbook reviewers praised books on quantum mechanics that “avoided philosophical discussion” or omitted “philosophically tainted questions.” The quarter century that followed witnessed an extraordinary buildup of calculating skill, but for every new calculation of baroque complexity that physics students learned to tackle they spent correspondingly less time puzzling through what all those fancy equations meant. “Shut up and calculate” became the new motto.¹ Richard Feynman famously warned students not to ask themselves “how can it be like that.” These were his exact words²:

If I say [electrons] behave like particles I give the wrong impression; also if I say they behave like waves.... They behave in a way that is like nothing that you have ever seen before.... There is one simplification at least. Electrons behave in this respect in exactly the same way as photons; they are both screwy, but in exactly the same way….

[I]t is essential to talk about this particular aspect. It will be difficult. But the difficulty really is psychological and exists in the perpetual torment that results from your saying to yourself, “But how can it be like that?” which is a reflection of uncontrolled but utterly vain desire to see it in terms of something familiar. I think I can safely say that nobody understands quantum mechanics. So do not take the lecture too seriously, feeling that you really have to understand in terms of some model what I am going to describe, but just relax and enjoy it. I am going to tell you what nature behaves like. If you will simply admit that maybe she does behave like this, you will find her a delightful, entrancing thing. Do not keep saying to yourself, if you can possibly avoid it, “But how can it be like that?” because you will get “down the drain,” into a blind alley from which nobody has yet escaped. Nobody knows how it can be like that.

Heedless of Feynman’s warning, a ragtag crew of young physicists banded together in the mid-1970s to ask themselves just that. In May 1975, two graduate students at the University of California at Berkeley founded an informal discussion group calling itself the Fundamental Fysiks Group. Anyone interested in the interpretation of quantum mechanics was welcome to attend their weekly meetings, which continued over the next three and a half years.

The group managed to cultivate patrons ranging from the Central Intelligence Agency to self-made entrepreneurs like Werner Erhard, guru of the fast-expanding human potential movement. With money pouring in from such unconventional sources, it carved out new institutional niches in which to pursue their big-picture discussions. Most influential was the Esalen Institute in Big Sur, California, fabled incubator of all things New Age.

At the same time, members of the Fundamental Fysiks Group started a flood of publications about “the new physics” and its implications. Many sold handsomely; some netted national awards. Best known today are The Tao of Physics (1975) by physicist and group member Fritjof Capra and The Dancing Wu Li Masters (1979) by Gary Zukav, at the time an avid participant in the group’s discussions. These efforts helped to bring sustained attention to the interpretation of quantum mechanics back into the classroom.

As Kaiser explains, the Fundamental Fysiks Group “saved” physics in three ways. First, they opened up space again for the kind of spirited philosophical engagement with fundamental physics that the Cold War decades had dampened. Second, they latched onto a topic, known as “Bell’s theorem,” and rescued it from a decade of unrelenting obscurity. They struggled to make sense of it and see what it might imply. In the process, they forced a few of their mainstream peers to pay attention to the topic, jousting with them over its ultimate implications. From these battles, quantum information science was born. Third, from the group’s tireless efforts to explore whether Bell’s theorem might unlock the secrets of telepathy, telekinesis, and extrasensory perception, there emerged the famous no-cloning theorem, which lays down that it is impossible to produce an exact copy, or clone, of a quantum state of which it is not known how it was prepared. The no-cloning theorem is what makes quantum encryption unbreakable. A quantum-encrypted message cannot be intercepted without making it undecipherable.

JSB v. EPR

In the late 1940s, as I have recounted in a previous post, John Steward Bell, having just obtained two bachelor's degrees at the University of Belfast, wondered whether hidden variables could be added to quantum mechanics. But when he learned that John von Neumann had “proved” that hidden variables could not be made compatible with quantum mechanics, he dropped the idea. Then, in 1952, he “saw the impossible done.” In that year David Bohm published two papers in which he suggested an interpretation of quantum mechanics in terms of hidden variables! Nevertheless, given the spirit of the time, Bell found it prudent to walk away from foundational questions — until he arrived at CERN, where he made the acquaintance of Josef Jauch, who at the time was trying to strengthen von Neumann’s proof! Thereupon he resolved to discover where von Neumann had erred. What he found was that von Neumann had made an assumption that Bell later described as “not just flawed” and “not merely false” but “silly” and “foolish.”

While Bohm’s theory reproduces the predictions of (non-relativistic) quantum theory, there is a price to pay: it is, in Bell’s words, “hideously nonlocal.” For instance, it implies that the trajectories of elementary particles “were instantaneously changed when anyone moved a magnet anywhere in the universe”.³ Bell decided to find out if this was a defect specific to Bohm’s theory or intrinsic to every hidden-variables theory consistent with quantum mechanics. (He hoped that it was the former.) The obvious test bed was the setup discussed by EPR.

In their renowned 1935 paper,⁴ Albert Einstein and his junior colleagues Boris Podolsky and Nathan Rosen (known from the start by the initials “EPR”) had argued that there are situations in which the simultaneous values of the position and the momentum of a particle could be determined with (theoretically) unlimited precision, and that therefore quantum mechanics was an incomplete theory, inasmuch as it implied, via uncertainty relations, that this could not be done.

EPR considered a source that emits a pair of particles of equal mass traveling with the same speed in opposite directions. This, they argued, made it possible to measure either the position or the momentum of the left-moving particle and deduce from the outcome the position or the momentum of the right-moving particle “without in any way disturbing” the latter. At the same time one could measure either the momentum or the position of the right-moving particle directly, and in this way determine both the position and the momentum of the right-moving particle, in apparent contradiction to the uncertainty principle.

Bohr, responding to EPR’s paper, argued that unless the position or the momentum of a particle was measured directly (rather than merely inferred from the outcome of another measurement), it was wrong to attribute to it a value. What the outcome of the measurement performed on the left-moving particle makes possible is to predict the outcome of the corresponding measurement performed on the right-moving particle. Even so, the question remains: how is it possible to make this prediction?

Einstein would argue, as he later did in a 1948 letter to Max Born⁵, that everything we regard as real must be localized in time and space. Furthermore:

When a system in physics extends over the parts of space A and B, then that which exists in B should somehow exist independently of that which exists in A. That which really exists in B should therefore not depend on what kind of measurement is carried out in part of space A; it should also be independent of whether or not any measurement at all is carried out in space A. If one adheres to this programme, one can hardly consider the quantum-theoretical description as a complete representation of the physically real. If one tries to do so in spite of this, one has to assume that the physically real in B suffers a sudden change as a result of a measurement in A. My instinct for physics bristles at this. However, if one abandons the assumption that what exists in different parts of space has its own, independent, real existence, then I simply cannot see what it is that physics is meant to describe.

Einstein takes it for granted that the outcome of a measurement performed in B is determined locally, by what exists or is real in B. Hence, if it is possible to predict the outcome of a measurement in B given the outcome of a measurement performed in A, the outcome of a measurement in A must somehow affect what exists or is real in B. “No reasonable definition of reality could be expected to permit this,” EPR declared in their paper. Because quantum theory “cannot be reconciled with the idea that physics should represent a reality in time and space, free from spooky actions at a distance,” Einstein could not “seriously believe” in it, as he wrote in another letter to Born⁶.

EPR’s paper concluded with these words:

While we have thus shown that [quantum mechanics] does not provide a complete description of the physical reality, we left open the question of whether or not such a description exists. We believe, however, that such a theory is possible.

In the final section of the paper⁷ in which he demolished von Neumann’s “silly” proof, Bell concluded that, in Bohm’s theory,

an explicit causal mechanism exists whereby the disposition of one piece of apparatus affects the results obtained with a distant piece. In fact the Einstein-Podolsky-Rosen paradox is resolved in the way which Einstein would have liked least.

In a subsequent paper,⁸ Bell showed that a causal mechanism of this kind is not specific to Bohm’s theory (as he himself had hoped) but is in fact intrinsic to every hidden-variables interpretation of quantum mechanics.

And then... nothing. Bell’s paper, deemed worthy of “the attention of all physicists” by the editors of the short-lived journal in which it appeared, did not receive a single citation in the literature for four long years — and then it was a passing mention in a one-page article. In 1971 six citations appeared, in 1972 seven, in 1973 three. The dam began to burst only in 1976, twelve years after the paper’s publication, when twenty to thirty new articles on the topic began to appear each year. The largest share of articles on Bell’s theorem during this period came from physicists working in the United States, and nearly three-quarters of these came from regular participants in the Fundamental Fysiks Group. By 1985, a “distinguished Princeton physicist” reportedly⁹ declared: “Anybody who’s not bothered by Bell’s theorem has to have rocks in his head.” And in 2011, after Bell’s theorem had been experimentally confirmed, Tim Maudlin wrote¹⁰:

For those interested in the fundamental structure of the physical world, the experimental verification of violations of Bell’s inequality constitutes the most significant event of the past half-century. In some way our basic picture of space, time, and physical reality must change. These results, and the mysteries they engender, should be the common property of all who contemplate with wonder the universe we inhabit.

Bell’s theorem at last

In a conversation with Jeremy Bernstein,¹¹ Bell recalled:

[EPR] ended their paper by stating that if you somehow completed the quantum-mechanical description, the nonlocality would only be apparent. The underlying theory would be local. So I explicitly set out to see if in some simple Einstein-Podolsky-Rosen situation I could devise a little model that would complete the quantum-mechanical picture and would leave everything local. I started playing around with the very simple system of two spin-1/2 particles, not trying to be very serious, but just to get some simple relations between input and output that might give a local account of the quantum correlations. Everything I tried didn’t work. I began to feel that it very likely couldn’t be done. Then I constructed an impossibility proof.

David Mermin has come up with what is arguably the simplest version of Bell’s impossibility proof.¹² Here goes.

The device at the center launches pairs of particles in opposite directions. Each particle enters an apparatus that can perform one of three measurements. Each measurement has two possible outcomes, indicated by a red or green light. In each run of the experiment the two measurements are randomly selected. After a large number of runs, we have in our hands two records of apparatus settings and outcome readings beginning, for instance, like this:

As predicted by quantum mechanics, the two records evince the following characteristics:

• Whenever both apparatuses perform the same measurement (11, 22, or 33), equal colors (RR or GG) are never observed.

• The pattern of R’s and G’s is completely random. This means, in particular, that the apparatuses flash different colors exactly half of the time.

If this does not bother you, then try to explain how it is that the colors invariably differ whenever identical measurements are made. Take your time.

There are some amusing illustrations of these correlations. Bell¹³ himself provided the following, complete with a hand-drawn figure.

Dr. Bertlmann likes to wear socks of different colours. Which sock he will have on a given foot on a given day is quite unpredictable. But when you see that the first sock is pink you can be already sure that the second sock will not be pink. Observation of the first, and experience of Bertlmann gives immediate information about the second.

What makes this particular scenario a test case for local hidden variables is that at most one of the three properties can be measured at any given time. In the EPR scenario, the properties which cannot be measured simultaneously are position and momentum. In Mermin’s scenario, the properties which cannot be measured simultaneously are the three components of the spins of the particles employed, each of which can take either of two values.

As mentioned at the beginning of this piece, there are two possible explanations of why (in the present scenario) the colors invariably differ whenever identical measurements are made. Because explanations involving instantaneous transmission of information are ruled out by relativity, we only need to consider common-cause explanations, and presently they involve the assumption that the particles carry instruction sets. An instruction set is a set of properties that determines how the apparatus will respond. Because the observed correlations are accounted for by instruction sets carried by particles launched at the same place, they have a local explanation.

If the common-cause explanation would work, it would be possible to think of each apparatus as revealing an intrinsic property of the incoming particle — a property whose existence in no way depends on being revealed by a measurement. Also the explanation would involve hidden variables, since no measurement or set of simultaneous measurements can reveal the values of more than one of the three spin components.

There are 2³ = 8 possible instruction sets: RRR, RRG, RGR, GRR, RGG, GRG, GGR, and GGG. If a particle arrives with, say, RGG then the apparatus flashes red if it is set to 1, and green if it is set to 2 or 3. To account for the strict correlation between the behaviors of the two apparatuses, the particles must carry opposite instruction sets: if one particle arrives with the instruction set RRG, the other particle arrives with GGR.

To find out whether this can account for the observed correlations, let us assume that the instruction sets are RRG and GGR. In this case we expect to see different colors with five of the 3² = 9 possible combinations of apparatus settings (11, 22, 33, 12, and 21), and we expect to see equal colors with four of them (13, 23, 31, and 32). Because the apparatus settings are randomly chosen, this pair of instruction sets thus produces different colors 5/9 of the time. The same will be true for the remaining pairs of instruction sets except for the pair RRR, GGG. If the two particles carry these instruction sets, we will see different colors every time, regardless of the apparatus settings. Bottom line: we will see different colors at least 5/9 of the time. The probability of observing different colors is equal to or greater than 5/9. This is Bell’s theorem.

In reality, the apparatuses flash different colors half of the time. The probability of observing different colors equals 1/2, which is less than 5/9. The common cause explanation, involving local hidden variables, is thereby ruled out.

In his renowned 1935 paper featuring his eponymous cat, Erwin Schrödinger expressed the view that “[m]easurements on separated systems cannot directly influence each other — that would be magic.” In 1964, Bell showed that the magic was real and inevitable.

1. This motto has been widely misattributed to Richard Feynman. It was actually coined by David Mermin, in his Physics Today “Reference Frame” column of April 1989, titled “What’s wrong with this pillow.”

2. R. Feynman, The Character of Physical Law, pp. 128–129 (The M.I.T. Press, 1967).

3. J. Bernstein, Quantum Profiles, p. 72 (Princeton University Press, 1991).

4. A. Einstein, B. Podolsky, and N. Rosen, Can quantum-mechanical description of physical reality be considered complete?, Physical Review 47, 777–780 (1935).

5. M. Born, The Born–Einstein Letters: Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955, p. 164 (Macmillan, 1971).

6. Op. cit., p. 158.

7. J.S. Bell, On the problem of hidden variables in quantum mechanics, Reviews of Modern Physics 38, 447–452 (1966). Though published after the 1964 paper below, it was actually written before it.

8. J.S. Bell, On the Einstein Podolsky Rosen paradox, Physics Physique Fizika 1 (3), 195–200 (1964).

9. N.D. Mermin, Is the moon there when nobody looks? Reality and the quantum theory, Physics Today 38 (4), 38–47 (1985).

10. T. Maudlin, Quantum non-locality and relativity, p. 4 (Wiley–Blackwell, 2011).

11. Bernstein, Quantum Profiles, pp. 72–73.

12. Mermin, Is the moon there when nobody looks?

13. Bertlmann’s Socks and the Nature of Reality, in: J.S. Bell, Speakable and Unspeakable in Quantum Mechanics, pp. 139–169 (Cambridge University Press, 1987).