Today I want to follow up on the two-slit experiment with electrons, which I introduced in my last mailing, and which according to a 2002 poll conducted by Physics World ranks as “the most beautiful experiment in physics.” The setup features an electron gun situated at G, a plate with two slits (L and R) equidistant from G, and a screen consisting of an array of detectors, one of which (at D) is shown in the following schematic.
What is observed in this experiment is the frequency of detections at the screen as a function of the detector position D. As the number of detected electrons increases, this function resembles more and more closely the probability of detection predicted by quantum mechanics. This probability depends on whether the set-up does or does not make it possible to find out, for each electron, through which slit it went. The following graph is predicted if this possibility exists:
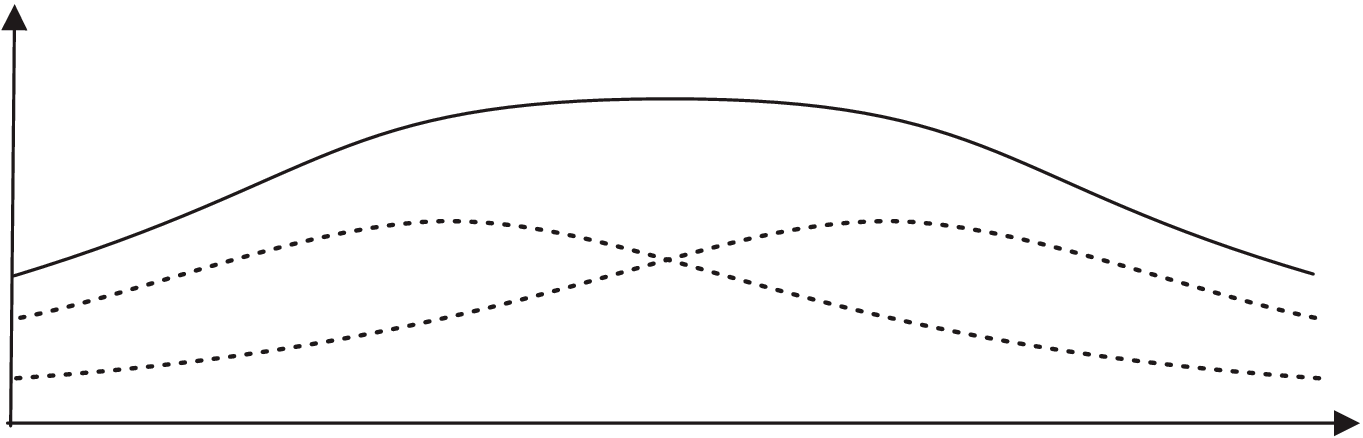
This is more or less what one would expect. If an event can come about in either of two ways, its probability is the sum of two probabilities, one for each of the two ways (in this case: getting to D via L and getting to D via R). The next graph is predicted if it is not possible to determine, for each electron, through which slit it went:
In 1989, Akira Tonomura and coworkers1 published the results of an experiment that was in all essential respects equivalent to a two-slit experiment. Because electrons were detected one at a time, it was possible to observe the buildup of the pattern of maxima and minima in real time:
If you are familiar with the mathematics of wave propagation, you may see in the second graph the interference pattern produced by a plane wave that has passed through a barrier with two gaps. Two waves — in this case, the two secondary waves emerging from the gaps — are said to “interfere constructively” wherever their respective crests or troughs meet. They are said to “interfere destructively” where a crest meets a trough or a trough meets a crest. Something like this seems to be going on here. Hence the notion that electrons sometimes behave like particles and sometimes like waves. The conclusion that can be usefully drawn from this, however, is not that electrons are weird or that quantum mechanics is weird — this goes without saying — but that the properties or behaviors of electrons and other so-called “constituents” of matter are contextual: they owe their meanings to the experimental conditions under which they are observed. Under one set of conditions, the slit taken by the electron can be known. Under another set of conditions, it cannot be known.
The contextuality of electrons and suchlike is the reason why quantum mechanics has two fundamental rules rather than just one. I am not referring to the old saw that wave functions have two modes of evolution: continuous between measurements and (generally) discontinuous at the time of a measurement. The wave function isn’t something that evolves, whether continuously or discontinuously. Its time dependence is a dependence on the time of the measurement to the possible outcomes of which it serves to assign probabilities, rather than the dependence on time of an evolving physical object or state. I am referring to these two fundamental rules:
If we want to calculate the probability of a particular outcome of a measurement M₂, given the actual outcome of an earlier measurement M₁, we must choose a sequence of measurements that may be made in the meantime, and we must do either of the following.
[Rule 1] If the intermediate measurements are made (or if it is possible to find out what their outcomes would have been), we must square the magnitudes of the amplitudes associated with all possible sequences of intermediate outcomes and add the results.
[Rule 2] If the intermediate measurements are not made (and it is not possible to find out what their outcomes would have been), we must add the amplitudes associated with all possible sequences of intermediate outcomes and square the magnitude of the result.
At this point I want you to simply appreciate the difference between the two rules. Rule 1 requires us to first square numbers and then add the results. Rule 2 requires us to first add numbers and then square the result. I also want you to appreciate the central roles played by measurements: not only do we assign probabilities to measurement outcomes on the basis of measurement outcomes, we also calculate these probabilities by invoking measurements that may or may not be made meantime.
In general we have a sequence of any number n of intermediate measurements. If each measurement has m possible outcomes, then there are mⁿ possible sequences of intermediate outcomes. These sequences are known as “alternatives.” (For example, if the electrons had to pass n=2 plates each with m=3 slits, there would be 3²=9 alternatives.) To each alternative we have to assign a complex number called “amplitude.” In the two-slit experiment, we have a single intermediate measurement with two possible outcomes, so there are two alternatives whose respective amplitudes we shall denote by A(L) and A(R).
There is no need to be scared of complex numbers. Just as the so-called real numbers (which are used to measure all manner of things) can be visualized as points on a straight line, so the complex numbers can be visualized as arrows in a plane. There are two ways to specify such an arrow:
In terms of its components with respect to two perpendicular axes, the real axis (which contains the real numbers) and the imaginary axis, so called because it contains the real numbers multiplied by something as imaginary as the square root of (‒1),
In terms of its magnitude (a real number) and the direction in which it points (specified by an angle that is called its “phase”).
To add two complex numbers, we add their components (with respect to each axis), and to multiply two complex numbers, we multiply their magnitudes and add their phases. It’s as easy as pie (with an “e”).
To be able to calculate the probability with which an electron launched at G will be detected at D, we need another three rules. What I want to impress on you now is that no empirical input is required to figure them out.2 Here they are:
[Rule 3] A(L) is the product of two complex numbers, the amplitude <D|L> for the electron to get from L to D and the amplitude <L|G> for the electron to get from G to L. By the same token, A(R) = <D|R> <R|G>.
[Rule 4] The magnitude of <B|A> (the amplitude for the electron to get from location A to location B) is inversely proportional to the distance d(B,A) between A and B.
[Rule 5] The phase of <B|A> is proportional to d(B,A).
So why is A(L) equal to the product of <D|L> and <L|G>? Here we assume that G, L, and D are exact positions. (Without this assumption the argument gets more messy, though the conclusion remains the same.) If the electron starts out from an exact position, we can invoke the previously discussed uncertainty relation:
Δr Δp ≧ h/(4π) .
If we reduce the position uncertainty Δr, we must increase the momentum uncertainty Δp to ensure that the product of the two uncertainties remains equal or greater than h/(4π). In the limit in which Δr approaches 0, Δp must approach infinity. Hence if the electron travels from A to C via an exact position B, it proceeds from B with a completely indeterminate momentum. Where the electron will be found subsequently is therefore independent of where it was previously found. Now, it is a fundamental rule of probability theory that the probability with which two independent events occur is the product of the probabilities of the individual events. Therefore the probability with which the electron gets first from L to D and then from G to L is the product of the probabilities pr(D|L) and pr(L|G).
We also need to know how an amplitude <B|A> is related to the corresponding probability pr(B|A). To this end we recall Rule 1, which now reads: if it is possible for each electron to determine the slit taken by it, then the probability of finding the electron at D is the sum of the squared magnitudes of the amplitudes A(L) and A(R):
pr(D|G) = |A(L)|² + |A(R)|².
As was mentioned already, the probability of an event that can come about in two ways is the sum of the probabilities assigned to these two ways:
pr(D|G) = pr(L) + pr(R).
Clearly, pr(L) equals |A(L)|² and pr(R) equals |A(R)|². But pr(L) (as we have seen) also equals the product of pr(D|L) and pr(L|G). Therefore A(L) equals the product of <D|L> and <L|G>.
On to Rule 4. Imagine a sphere of radius R. Let pr(R) be the probability with which a particle launched at the center C of the sphere will be found by a detector that monitors a unit area of the surface S of the sphere. Because the particle proceeds from C in no particular direction — meaning it is equally likely to be found having traveled in any direction from C — pr(R) is constant over S. If S is covered with detectors that jointly monitor the entire sphere, the probability with which the particle will be detected somewhere on S (no matter where) equals 1. Because the surface area of a sphere is proportional to the square of R, pr(R) will be inversely proportional to the square of R. And because probabilities are the squared magnitudes of amplitudes, the corresponding amplitude will be inversely proportional to R. In other words, the magnitude of <B|A> will be inversely proportional to the distance d(B,A).
Moving on to Rule 5, because a particle launched at A is as likely to proceed in one direction as in any other, the phase of <B|A> cannot depend on the direction in which the particle is found to proceed. It can only depend on the distance d(B,A). To find out how it depends on d(B,A), we need to remember that distances are not built into space. It is we who decide how distances are measured, and in this we are guided by convenience. As was stressed by Henri Poincaré, “one geometry cannot be more true than another, it can only be more convenient.” So which geometry is the most convenient? Newton himself appears to have been aware of the problem, writing as he did that
the description of right lines and circles, upon which geometry is founded, belongs to mechanics. Geometry does not teach us to draw these lines, but requires them to be drawn.3
To Newton, the most convenient geometry was that in which straight (right) lines are “drawn” by freely moving bodies. In a quantum world, where freely moving particles do nothing as mundane as following straight lines, the most convenient choice is to let equal distances correspond to equal phases. This is why the phase of <B|A> is proportional to d(B,A).
We now have all the rules that are needed to calculate the distribution of electron detections in two-slit experiments with electrons. And all we needed to figure them out were the first two rules, which involve nothing but statistical correlations between measurement outcomes and the manner in which they are combined in two different experimental contexts.
After the publication of the first edition of my textbook, the following (unsolicited) review was posted on Amazon. It is probably the only book with a five-star review that says, “You will hate this book”:
Richard Feynman famously stated “I think it is safe to say that no one understands Quantum Mechanics.” This book is changing that.... Reading chapter 5 has been a most humbling experience. I studied physics and have always been captivated by the particle wave dualism that the classical two slit experiment embodies so beautifully.... The way this book covers the two slit experiment everything falls into place and makes perfect sense. There is no wave particle dualism, just the naked necessity of a probabilistic regime. It is so simple. Painfully obvious. Easy to grasp with just a minimum of mathematical rigor. It boggles the mind that QM has not been understood this way from the get go. This feels like 20/20 hindsight writ large.... If you’ve been trying to make sense of QM you will hate this book. It’ll make you feel stupid for not having been able to see this all along. Time to eat some humble pie.
Thank you, Henning.
A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, and H. Ezawa, Demonstration of single-electron buildup of an interference pattern, American Journal of Physics 57 (2), 117‒120 (1989).
Almost the same can be said of the first two rules, though it takes more time and effort to demonstrate this.
Sir Isaac Newton's Mathematical Principles of Natural Philosophy and His System of the World, English translation of Philosophiae naturalis principia mathematic by A. Motte, revised by A. Cajori, 1729 (University of California Press, 1934).





