The shapes of things
Quantum mechanics is the first physical theory that accounts for the existence of form
Every thing in visual experience is spatially extended and therefore conceptually divisible by cutting. The literal meaning of the Greek word ἄτομος is “uncuttable.” The reason it is usually translated as “indivisible” is that, until quantum mechanics came along, the ultimate parts of material objects were defined by boundaries, while the form of a not further divisible object was conceived as the boundary separating a “stuff-filled” inside from an empty outside (imagine three-dimensional cookie cutters).
While Plato believed that the Universe could be described using five simple shapes — the solids named after him — he could not account for the origin of these primordial shapes. The Greek atomists held that atoms came in an infinite variety of sizes and shapes, which likewise remained unaccounted for. Newton1 speculated that
God in the Beginning form’d matter in solid, massy, hard, impenetrable, moveable Particles, of such Sizes and Figures, and with such other Properties, and in such Proportion to Space, as most conduced to the end for which he form’d them,
and he (Newton) left it at that. The first physical theory that successfully accounts for the shapes of (inanimate) things is quantum mechanics. If a quantum object has a form, this consists of indefinite spatial relations between its component parts. And if a quantum object lacks component parts, it also lacks a form. What quantum mechanics removes from all earlier conceptions of form is the closed boundary that was supposed to be filled with “stuff.” In so doing it also removes the most vulgar conception of matter or substance. What quantum mechanics adds to earlier conceptions of form is that the ultimate, not further divisible parts are formless, and that the spatial relations between component parts are indefinite or fuzzy.
Why formless? According to the current (so-called) standard model of particles and forces, certain quantum objects, such as electrons and quarks, are fundamental in the sense that they are not composed of other quantum objects. While such objects are often described as pointlike (and many physicists take this to be the literal truth), this can only mean that they lack internal structure, which is another way of saying that they lack component parts and therefore are formless.
Why fuzzy? What is meant by characterizing a physical quantity as fuzzy or indefinite is that it can only be described by assigning probabilities to the possible outcomes of a (not actually performed) measurement of its value. For an illustration take another look at the indefinite position of the electron relative to the proton in some stationary states of atomic hydrogen (previously discussed in this post). The density of each of these “probability clouds” at any given point represents the probability (per unit volume) of finding the electron at that point.
Each of the possible forms of a bipartite quantum object (such as the hydrogen atom) consists of a single indefinite relative position. It is important to understand how these forms are defined. Apart from determining the probabilities of the possible outcomes of a measurement of the relative position between the two components, such a form is in turn determined by the outcomes of actual (or hypothetical) measurements, specifically those of the object’s energy, its total angular momentum, and one of the components of its angular momentum. (This is another illustration of the fact that at bottom quantum mechanics concerns statistical correlations between measurement outcomes.)
The (abstract, non-visualizable) form of a quantum object with N components consists of N(N-1)/2 indefinite relative positions. The forms of nucleons, nuclei, atoms, and molecules “exist” in probability spaces of increasingly higher dimensions. At the molecular level of complexity a different kind of form emerges: a three-dimensional form that can be visualized, and this not merely as a distribution over a probability space. I am referring to the configurations of molecules (that is, the spatial arrangements of their constituent atoms). What renders these configurations visualizable is that the indefiniteness of the distance between any pair of bonded atoms, as measured by the standard deviation of the corresponding probability distribution, is in general significantly smaller than the mean value of this distribution.
The shapes defined by quantum mechanics belong to types or species of objects. The next question to be addressed, therefore, concerns the individuation of quantum objects. The word “individuation” has two distinct meanings. The first concerns the manner by which a type of object comes to be an individual instance of that type. The second concerns the possibility of identifying two instances of the same type of object as the same individual object.
Regarding the second meaning, we have seen (in this post) that, in Schrödinger’s words, “the question of ‘sameness,’ of identity, really and truly has no meaning.” If a particle track is observed in a bubble chamber or some other detection device, it is overwhelmingly likely that the events constituting the track indicate the presence of the same particle, but it is never certain; the probability for this never equals 1. While, therefore, it is permissible “for all practical purposes”2 to talk as if the detection events indicated the passage of the same particle, it cannot be the literal truth. It is a concession to the object-oriented language of classical discourse.
It can, however, be used to determine the type to which a track belongs. This takes us to the other meaning of “individuation,” which concerns the manner by which a type of object comes to be an individual instance of its type. Contrary to the manner in which types are instantiated in ontologies of the Platonic/Aristotelean kind, the types that are defined by particle physics are instantiated neither by some principle called “matter” nor by persistent, re-identifiable, property-carrying substances. They are instantiated by sequences of events (“clicks”) that constitute tracks. Ole Ulfbeck and Aage Bohr3 had it exactly right when they wrote that “clicks can be classified as electron clicks, neutron clicks, etc.” even though “there are no electrons and neutrons on the spacetime scene.” Ditto Schrödinger when he wrote: “When you observe a particle of a certain type, say an electron, now and here, this is to be regarded in principle as an isolated event.”
Thus, not only the properties of quantum objects but also the quantum objects themselves are contextual. The properties of quantum objects are defined by the experimental contexts in which they are observed, and they only exist if and when they are observed. Quantum objects in turn are defined as bundles of intrinsic properties — properties like mass, spin, and electric charge — and they only exist if and when the presence of their characteristic properties is indicated by an experimental apparatus. As philosopher of science Brigitte Falkenburg4 wrote,
only the experimental context (and our ways of conceiving of it in classical terms) makes it possible to talk in a sloppy way of quantum objects.... [Quantum objects] seem to be Lockean empirical substances, that is, collections of empirical properties which constantly go together. However, they are only individuated by the experimental apparatus in which they are measured or the concrete quantum phenomenon to which they belong. [pp. 205‒206]
Quantum concepts refer to the properties of quantum phenomena which occur by means of a given experimental setup in a given physical context. [p. 200]
The carrier of these properties is nothing but the quantum phenomenon itself, say, a particle track on a bubble chamber photograph or the interference pattern of the double slit experiment. [p. 200]
As said, a track can be used to determine the type of particle that is instantiated by it. From a track one can deduce its radius of curvature in a magnetic field, the particle’s time of flight between consecutive clicks, its kinetic energy, and its energy loss through ionization and/or excitation. Measuring three of these four quantities is sufficient in principle to positively identify the particle type, which then makes it possible to classify the individual clicks as “electron clicks, neutron clicks, etc.”5 That the quantities which can be deduced from a track are more easily named in the language of persistent, re-identifiable objects (“the particle’s time of flight”, “its kinetic energy,” etc.) reflects our ineluctable dependence on the object-oriented language of classical discourse, no matter how ill-suited it may be.
When I wrote that object types are defined as bundles of intrinsic properties, I referred to the distinction between intrinsic and extrinsic properties in a specifically quantum-mechanical sense. The usual (pre-quantum) distinction is between properties that an object has in virtue of the way it is “in itself” and properties that it has in virtue of how it interacts with, or is otherwise related to, the rest of the world. Mass (or rest-energy) would be an example of an intrinsic property, while weight would be an example of an extrinsic property.
In the context of quantum mechanics, intrinsic properties are those that are characteristic of an object type, while extrinsic properties are those that an individual quantum object of a given type may or may not possess, such as being inside a particular region of space or having a spin pointing along a given axis. A quantum object has no way of being something “in itself.” All of its properties are contextual, the intrinsic ones no less than the extrinsic ones. While extrinsic properties like positions and spin components are instantiated with the help of devices like counters and Stern-Gerlach apparatuses, the type-defining intrinsic properties are instantiated with the help of devices ranging from photographic emulsions and small bubble chambers to CERN’s Large Hadron Collider.
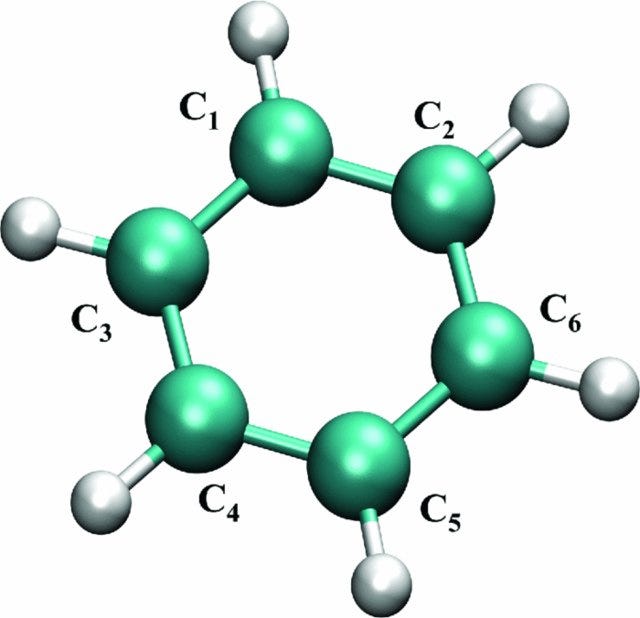
What about a composite quantum object like, say, a molecule of benzene? This, too, exists as an individual instance of the object type “benzene” only if the presence of its intrinsic properties is indicated by, for instance, a measurement of the frequencies at which it emits or absorbs radiation. And what about the atoms of carbon and hydrogen of which the benzene molecule is composed? Or the electrons and nucleons of which these atoms are composed? Even if their presence as instances of the object types “carbon” and “hydrogen” (or “electron”, “proton” and “neutron”) is not directly observed — by observing their respective intrinsic properties — we can infer it through our knowledge (both theoretical and experimental) of these object types.
I have claimed that quantum mechanics is the first physical theory that successfully accounts for the shapes of things. Leaving aside the question of living things, does quantum mechanics actually account for molecular structure — the shapes of the smallest things that can be visualized? The matter appeared settled when Paul Dirac6 declared in 1929 that
[t]he underlying laws necessary for the mathematical theory of a larger part of physics and the whole of chemistry are thus completely known, and the difficulty is only that exact applications of these laws lead to equations, which are too complicated to be soluble.
A reversal of opinion took place in the 1960s and ’70s, when the likes of Karl Popper, Thomas Kuhn, Imre Lakatos, and Paul Feyerabend challenged the prevailing view that the various special sciences could be reduced to physics. It became almost politically incorrect to hold reductionist views about any of the special sciences such as chemistry. It was argued that there are principled difficulties in accommodating molecular shape within quantum mechanics. Specifically, it was shown that one of the concepts underlying the description of the quantum states of molecules — the so-called Born-Oppenheimer approximation — effectively adds structure by hand. Yet in 2016 Eric Scerri,7 a prominent voice in the philosophy of chemistry, having acknowledged that chemistry “is popularly believed to be reducible, and indeed to have been reduced,” writes:
Let me quickly say that I now believe that this view is essentially correct and that chemistry is more or less a reduced science.... In this chapter I will be looking ... especially at parts of chemistry which I personally claimed as examples of the breakdown of reduction but on which I have now changed my opinion as a result of more recent research.
We have to leave it at that.
Fun fact: A molecule of ammonia (NH₃) is usually found in a coherent superposition of two mirror-symmetric configurations (one in which the nitrogen atom is situated on one side of the plane defined by the three hydrogen atoms, and one in which the nitrogen atom is situated on the other side of that plane), which is a non-visualizable state of affairs. A molecule of sugar, on the other hand, is always found in either of two mirror-symmetric configurations, one known as “glucose” and the other known as “fructose.” In fact, most molecules save the smallest ones are generally observed with their atomic nuclei in definite (hence visualizable) configurations, and hardly ever in non-visualizable superpositions of distinct configurations.
How so? The answer is environmental decoherence, which has been discussed in this post. If a sugar molecule’s interaction with the rest of the world could be switched off, it should be possible in principle to prepare it in a coherent superposition of glucose and fructose, but if the interaction were then switched back on, it would at once get entangled with the rest of the world. Its quantum state would decohere in about a billionth of a second into an equiprobable mixture of the environmentally stable states glucose and fructose. In practical terms this means that any measurement of the state of a sugar molecule will yield either glucose or fructose as its result.
What distinguishes the shapes of quantum objects (including sugar molecules) from the shapes of classical objects — the shapes of things that are directly accessible to human sensory experience? Ψ-ontologists invoke environment-induced decoherence to explain why even a sugar molecule is objectively either glucose or fructose. The probability with which we shall find it in a superposition of glucose and fructose is so miniscule that it can be ignored. We can interpret its quantum state as a statistical mixture and think of it as an ensemble whose members are either glucose or fructose. This is another instance of what John Bell has called the “FAPP trap”,8 where “FAPP” is his acronym for “for all practical purposes.” Ψ-ontology makes it possible to say that FAPP an actual molecule of sugar is either glucose or fructose but, in truth, Ψ-ontology cannot even explain how it is possible for measurements to have outcomes. What actually distinguishes the shapes of classical objects from those of quantum objects is that the former are accessible to direct sensory experience, while the latter are not.
In can hardly be contested that human beings are able to communicate with each other in a public language. But this means that there are publicly available objects of reference. In classical physics, the publicly available objects of reference are substances in the Kantian sense of persistent carriers of properties which interact and change in accordance with causal laws. In quantum physics, one has to distinguish between two kinds of objects: classical objects, which like all objects in classical physics are (or can be assumed to be) directly accessible to human sensory experience, and quantum objects, which “are only individuated by the experimental apparatus in which they are measured or the concrete quantum phenomenon to which they belong.” The former include experimental arrangements and measurement devices. Because the latter are not accessible to direct sensory experience, they cannot be expected to conform to the spatiotemporal conditions of human sensory experience, and therefore cannot be expected to be accurately describable in any language that we can understand. They can be spoken of only indirectly, in terms of experiments and their results, or else in the sloppy FAPP way.
I. Newton, Opticks, Query 31 (printed for W. Innys, 1730).
On the frequent occurrence of this expression in the literature on quantum mechanics see this post.
O. Ulfbeck and A. Bohr, Genuine Fortuitousness. Where Did That Click Come From? Foundations of Physics 31, 757‒774 (2001).
B. Falkenburg, Particle Metaphysics: A Critical Account of Subatomic Reality (Springer, 2007).
C. Grupen and B. Shwartz, Particle Detectors, Chapter 9 (Cambridge University Press, 2008).
P.A.M. Dirac, Quantum mechanics of many-electron systems, Proceedings of the Royal Society A 123, 714–733 (1929).
E.R. Scerri, The Changing Views of a Philosopher of Chemistry on the Question of Reduction, in E.R Scerri and G. Fisher (Eds.), Essays in the Philosophy of Chemistry, pp. 125–143 (Oxford University Press, 2016).
When, at the 1990 conference “Sixty-Two Years of Uncertainty,” David Mermin spoke up in defense of Kurt Gottfried’s position on standard quantum theory, Bell snapped “FAPP trap.” Recounted by Philip Pearle (Tales and Tails and Stuff and Nonsense, in R.S. Cohen, M.A. Horne, and J.S. Stachel (Eds.), Experimental Metaphysics-Quantum Mechanical Studies in Honor of Abner Shimony Vol. 1, Kluwer, pp. 143–156, 1997).