A central mystery of physics

The miraculous identity of particles (not only) of the same type

Imagine that in front of you there are two exactly similar objects. All their properties are the same, except that they are in different places. Because they are in different places, they are different objects. But is the fact that they are in different places the sole reason why they are different objects? Or is there another reason?

John Duns Scotus, an influential philosopher-theologians of the High Middle Ages, thought that there was another reason. Earlier scholastic philosophers had defined “matter” in two mutually contradictory ways: as what is the same in all actually existing things, and as what is different in all exactly similar things. As what is the same in all actually existing things, matter betokened the actual existence of things, and as what is different in all exactly similar things, matter betokened the individuality of things. To relieve matter of the second job, Scotus invented a property called “haecceity” or “thisness.” (Haec is the nominative feminine of the Latin word for “this.”)

But haecceity does not actually answer the question. Demonstrative determiners like “this” and “that” distinguish things by pointing at them, which is to say by the different locations at which they are situated. Citing their being at different locations as the reason why two exactly similar things are different things, does not answer the question whether being situated at different locations is the sole reason for their being different things.

Let’s try another tack. We may invoke the philosophical principle of the identity of indiscernibles, according to which two exactly similar objects are numerically identical; they are one and the same thing under different aspects or names. “Barack Obama” and “the 44th president of the United States” refer to the same person, as do “Clark Kent” and “Superman.” On this account, two exactly similar things in different places ought to be regarded as one and the same thing under different aspects, which sounds absurd.

It might be argued that the question does not arise; there are no exactly similar things. Between any two objects there are always differences, however minute. While this is true for macroscopic objects, it is not true for subatomic particles. Two electrons in different places have exactly the same properties, apart from being in different places. Richard Feynman made extensive and fruitful use of the idea that even an electron and a positron are one and the same thing, except that the positron moves backward in time. In his Nobel Acceptance Lecture, he recounted the following story:

I received a telephone call one day at the graduate college at Princeton from Professor Wheeler, in which he said, “Feynman, I know why all electrons have the same charge and the same mass.” “Why?” “Because, they are all the same electron!”

---

In an earlier mailing, which can be retrieved here, I discussed a series of position measurements, in which each measurement yields exactly one outcome — each time exactly one counter clicks. The point of the discussion was to illustrate a connection between conservation laws and persistence through time. The behavior of the counters provides evidence of a conservation law, the conserved quantity being the number N of simultaneous clicks. In this particular case (N = 1), it can be interpreted as evidence of an object that persists through time.

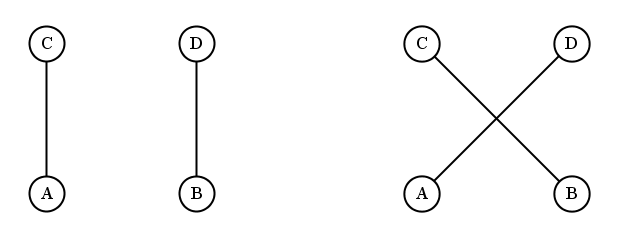
If we perform a series of position measurements and each time exactly two counters click, we have evidence of the same conservation law (with N = 2), but if this is the only conservation law in force, we cannot interpret the number of simultaneous clicks as evidence of two persistent objects. To understand why not, consider the following setup. Initially two counters click, indicating the presence of a particle at A and a particle at B. The next thing we observe is that another two counters click, indicating the presence of a particle at C and a particle at D. As illustrated in the drawing below, there are two alternatives: either the particle detected at A is identical with the particle detected at C (in which case the particle detected at B is identical with the particle detected at D) or the particle detected at A is identical with the particle detected at D (in which case the particle detected at B is identical with the particle detected at C).

If we want to calculate the probability with which the counters at C and at D click right after the counters at A and at B have clicked, we must (as previously explained) apply either of two rules. If it is possible to find out which alternative has taken place, we must apply the first rule, which stipulates that we first square the magnitudes of the amplitudes associated with the alternatives and then add the results. The second rule applies if it is not possible to find out which alternative has taken place, and it stipulates that we first add the amplitudes and then square the magnitude of the result. Because the resulting probabilities generally differ, we cannot assume that either alternative has taken place when it is not possible to find out which alternative has taken place.

What would make it possible (in this particular situation) to find out which alternative has taken place, is the existence of “identity tags” — conserved quantities by which the particles can be distinguished and re-identified. Returning to our previous setup (a series of position measurements), we are free to infer the presence of two persistent particles if and only if each time one of the detected particles is found to carry property X while the other is found to carry property Y, where X and Y are any pair of distinct conserved quantities.

---

In situations in which we add amplitudes rather than probabilities, it is meaningless to ask: which of the initially detected particles is identical with which of the subsequently detected particles? Here as elsewhere, the challenge is to learn to think in ways that do not lead to meaningless questions. One strategy to avoid the meaningless question “Which is which?” is Schrödinger’s,¹ who insisted that “the ultimate constituents of matter have no ‘sameness’ at all”:

If I observe a particle here and now, and observe a similar one a moment later at a place very near the former place, not only cannot I be sure whether it is “the same,” but this statement has no absolute meaning.... We assume — following a habit of thought that applies to palpable objects — that we could have kept our particle under continuous observation, thereby ascertaining its identity. This habit of thought we must dismiss. We must not admit the possibility of continuous observation. Observations are to be regarded as discrete, disconnected events. Between them there are gaps which we cannot fill in. There are cases where we should upset everything if we admitted the possibility of continuous observation. That is why I said it is better to regard a particle not as a permanent entity but as an instantaneous event.

In support of Schrödinger’s view, one may invoke the contextuality of quantum mechanics, which came up in several previous mailings. Primarily it refers to the fact that the properties of microscopic (or quantum) objects (i) are defined by the macroscopic apparatuses by which they are indicated and (ii) only exist if they are indicated. But it also pertains to the objects themselves. To see this, the relevant question to ask is: how does a quantum object, considered as a kind, species, or type, get individuated?

This echoes the age-old metaphysical question of how a One becomes Many. Plato, Aristotle, and virtually all subsequent philosophers worth their salt reflected on how the idea or concept of (say) a horse is related to the individual living and breathing horse. In traditional Western metaphysics, individuation was conceived as running parallel to predication: an immaterial essence or predicable universal becomes instantiated as a material individual that cannot be predicated of anything else. Matter, partaking of horseness, becomes an individual horse, or the idea of a horse becomes a physical horse by being placed in physical space. In the case of quantum objects, the instantiating medium is neither matter nor physical space but the experimental conditions in which they are observed.

These conditions do not permit continuous observation. Each click, each particle detection, is a separate event. Between such events there obtain statistical correlations, and these involve conservation laws. In exceptional situations, under specific experimental conditions, the conservation laws make it possible to entertain the illusion that we are repeatedly observing the same individual particle (rather than merely the same type of particle). “Sometimes these events form chains that give the illusion of permanent beings,” Schrödinger wrote, “but only in particular circumstances and only for an extremely short period of time in every single case.” The interpretation of such chains as permanent beings, therefore, is but a futile attempt to make quantum phenomena conform to the object-oriented language of classical discourse.

It is, moreover, based on a misunderstanding of the meaning of conservation laws. A conserved quantity is not something that needs to be carried continuously from an event by which its value or presence is indicated to the next such event. Instead, it is something that turns out the same each time it is measured on an isolated system. In the case of a non-relativistic isolated system, the number of simultaneous clicks is one of the conserved quantities. In the case of a relativistic system, this number can come out different each time it is measured. In a relativistic scattering event, for example, the number of outgoing particles can differ from the number of incoming particles. In either case, though, the total value of a conserved quantity like electric charge remains constant.

---

Another strategy to avoid the meaningless question is to go to the opposite extreme and insist, with Wheeler and Feynman, on the numerical identity of all particles of the same type (i.e., all particles that lack properties by which they can be distinguished). On this view, the question “Which is which?” arises because we assume, falsely, that initially there are two things, one located at A and another located at B, and that subsequently there are again two things, one located at C and another located at D. If there is only one thing, initially located at both A and B and subsequently located at both C and D, the meaningless question cannot be asked. If, on this view, we say that there are two things with two distinct properties, we use the word “two” once too often.

What’s more, the “miraculous identity of particles of the same type,” which according to Charles Misner, Kip Thorne, and John Wheeler² “must be regarded, not as a triviality, but as a central mystery of physics,” need not be confined to particles of the same type.

To see this, suppose what is initially detected is a particle of type X at A and a particle of type Y at B, and what is subsequently detected is a particle of type X at C and a particle of type Y at D. In the absence of the identity tags X and Y, we would be demonstrably wrong to insist that the particle at A is either the same as the particle at C or the same as the particle at D. The presence of identity tags, on the other hand, in no wise prevents us from asserting that there is just one thing, which initially is located both at A (as a particle of type X) and at B (as a particle of type Y), and which subsequently is located both at C (as a particle of type X) and at D (as a particle of type Y). There is no compelling reason to believe that the “miraculous identity” of particles ceases when it ceases to have observable consequences due to the presence of identity tags. We are free to take the view that the particle observed here with these properties and the particle observed there with those properties are one and the same thing. And if we go along with the idea that particles are the ultimate constituents of the experiential world, we can arrive at the conclusion that the number of ultimate constituents of this world is one.

But there is more. Every measurement, as was noted in this post, is genuinely fortuitous not merely with regard to its particular outcome but, more importantly, with regard to its actual occurrence. In particular, every position-indicating event is, in the words of Ole Ulfbeck and Aage Bohr,³ an event that “comes by itself, out of the blue” and is “entirely beyond law.” As these authors have stressed, genuinely fortuitous events, occurring by themselves, form “the basic material that quantum mechanics deals with.”

While, therefore, we cannot attribute clicks and other position-indicating events to causal agents within the experiential world, we can attribute them to a single causal agent beyond this world. And if we adhere to the principle of causality, according to which every event has a cause, we are bound to acknowledge the existence beyond this world of a causal agent that is responsible for all property-indicating events within this world. And if we acknowledge the existence of this causal agent, we can also look upon it as the ultimate constituent of the experiential world.

1. Science and Humanism, in E. Schrödinger, Nature and the Greeks and Science and Humanism, pp. 103‒171 (Canto Classics, 2014).

2. C.W. Misner, K.S. Thorne, and J.A. Wheeler, Gravitation, p. 1215 (Freeman, 1973).

3. O. Ulfbeck and A. Bohr, Genuine Fortuitousness. Where Did That Click Come From? Foundations of Physics 31, 757‒774 (2001).